题目内容
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 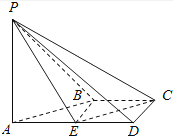
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
【答案】
(1)
解:延长AB交直线CD于点M,∵点E为AD的中点,∴AE=ED= ![]() AD,
AD,
∵BC=CD= ![]() AD,∴ED=BC,
AD,∴ED=BC,
∵AD∥BC,即ED∥BC.∴四边形BCDE为平行四边形,即EB∥CD.
∵AB∩CD=M,∴M∈CD,∴CM∥BE,
∵BE平面PBE,∴CM∥平面PBE,
∵M∈AB,AB平面PAB,
∴M∈平面PAB,故在平面PAB内可以找到一点M(M=AB∩CD),使得直线CM∥平面PBE
(2)
解:如图所示,

∵∠ADC=∠PAB=90°,异面直线PA与CD所成的角为90°,AB∩CD=M,
∴AP⊥平面ABCD.
∴CD⊥PD,PA⊥AD.
因此∠PDA是二面角P﹣CD﹣A的平面角,大小为45°.
∴PA=AD.
不妨设AD=2,则BC=CD= ![]() AD=1.∴P(0,0,2),E(0,1,0),C(﹣1,2,0),
AD=1.∴P(0,0,2),E(0,1,0),C(﹣1,2,0),
∴ ![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(0,1,﹣2),
=(0,1,﹣2), ![]() =(0,0,2),
=(0,0,2),
设平面PCE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 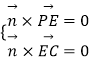 ,可得:
,可得: ![]() .
.
令y=2,则x=2,z=1,∴ ![]() =(2,2,1).
=(2,2,1).
设直线PA与平面PCE所成角为θ,则sinθ= ![]() =
=  =
= ![]() =
= ![]() .
.
【解析】(1)延长AB交直线CD于点M,由点E为AD的中点,可得AE=ED= ![]() AD,由BC=CD=
AD,由BC=CD= ![]() AD,可得ED=BC,已知ED∥BC.可得四边形BCDE为平行四边形,即EB∥CD.利用线面平行的判定定理证明得直线CM∥平面PBE即可.
AD,可得ED=BC,已知ED∥BC.可得四边形BCDE为平行四边形,即EB∥CD.利用线面平行的判定定理证明得直线CM∥平面PBE即可.
(2)如图所示,由∠ADC=∠PAB=90°,异面直线PA与CD所成的角为90°AB∩CD=M,可得AP⊥平面ABCD.由CD⊥PD,PA⊥AD.因此∠PDA是二面角P﹣CD﹣A的平面角,大小为45°.PA=AD.不妨设AD=2,则BC=CD= ![]() AD=1.可得P(0,0,2),E(0,1,0),C(﹣1,2,0),利用法向量的性质、向量夹角公式、线面角计算公式即可得出.
AD=1.可得P(0,0,2),E(0,1,0),C(﹣1,2,0),利用法向量的性质、向量夹角公式、线面角计算公式即可得出.
本题考查了空间位置关系、空间角计算公式、法向量的性质,考查了空间想象能力、推理能力与计算能力,属于中档题.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握空间角的异面直线所成的角(已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.

 灵星计算小达人系列答案
灵星计算小达人系列答案
