题目内容
【题目】在平面内,定点A,B,C,D满足 ![]() =
= ![]() =
= ![]() ,
, ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() =﹣2,动点P,M满足
=﹣2,动点P,M满足 ![]() =1,
=1, ![]() =
= ![]() ,则|
,则| ![]() |2的最大值是( )
|2的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:由 ![]() =
= ![]() =
= ![]() ,可得D为△ABC的外心, 又
,可得D为△ABC的外心, 又 ![]()
![]() =
= ![]()
![]() =
= ![]()
![]() ,可得
,可得![]() (
( ![]() ﹣
﹣ ![]() )=0,
)=0, ![]() (
( ![]() ﹣
﹣ ![]() )=0,即
)=0,即 ![]()
![]() =
= ![]()
![]() =0,即有
=0,即有 ![]() ⊥
⊥ ![]() ,
, ![]() ⊥
⊥ ![]() ,可得D为△ABC的垂心,
,可得D为△ABC的垂心,
则D为△ABC的中心,即△ABC为正三角形.
由 ![]()
![]() =﹣2,即有|
=﹣2,即有| ![]() ||
|| ![]() |cos120°=﹣2,解得|
|cos120°=﹣2,解得| ![]() |=2,△ABC的边长为4cos30°=2
|=2,△ABC的边长为4cos30°=2 ![]() ,
,
以A为坐标原点,AD所在直线为x轴建立直角坐标系xOy,
可得B(3,﹣ ![]() ),C(3,
),C(3, ![]() ),D(2,0),由
),D(2,0),由 ![]() =1,可设P(cosθ,sinθ),(0≤θ<2π),由
=1,可设P(cosθ,sinθ),(0≤θ<2π),由 ![]() =
= ![]() ,可得M为PC的中点,即有M(
,可得M为PC的中点,即有M( ![]() ,
, ![]() ),则|
),则| ![]() |2=(3﹣
|2=(3﹣ ![]() )2+(
)2+( ![]() +
+ ![]() )2=
)2= ![]() +
+ ![]() =
= ![]() =
= 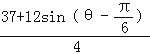 ,当sin(θ﹣
,当sin(θ﹣ ![]() )=1,即θ=
)=1,即θ= ![]() 时,取得最大值,且为
时,取得最大值,且为 ![]() .
.
故选:B.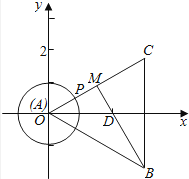

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目