��Ŀ����
����Ŀ����ij�������Ĺ۲��Ԥ�⣺������M�ص�ɳ����һֱ�����Ϸ����ƶ������ƶ��ٶ�v(km/h)��ʱ��t(h)�ĺ���ͼ����ͼ��ʾ�����߶�OC��һ��T(t,0)������Ĵ���l������OABC��ֱ��l��ಿ�ֵ������ʱ��t(h)��ɳ������������·��s(km)��

(1)��t��4ʱ����s��ֵ��
(2)��s��t�仯�Ĺ�������ѧ��ϵʽ��ʾ������
(3)��N��λ��M�����Ϸ����Ҿ�M��650 km�����ж��ⳡɳ�����Ƿ����Ϯ��N�ǣ�����ᣬ��ɳ����������ʱ��������Ϯ��N�ǣ�������ᣬ��˵�����ɣ�
���𰸡���1��24����2��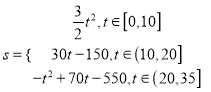 ����3��ɳ��������30 h����Ϯ��N�ǣ�
����3��ɳ��������30 h����Ϯ��N�ǣ�
�������������������1��������߶�OA�Ľ���ʽΪv=4t��Ȼ���t=10ֱ�Ӵ��������ʱ���ٶȣ��������S��t����ֵ����2���ȷֶ�����ٶ�v��ʱ��t�ĺ���������ϵ���ٷֱ����ʱ�伴����ö�Ӧ�ĺ���S��t���Ľ���ʽ����3�����ɷֶκ����Ľ���ʽ�Լ���Ӧ�Ķ����������������ֵ�����������ֵ����650�������½��ۻ���Ϯ��N�ǣ��ٰ�S��t��=650���뼴�������Ӧ��t��
����������⣺��1����ͼ���֪����t��4ʱ��v��3��4��12��
����S��![]() ��4��12��24 km��
��4��12��24 km��
��2����0��t��10ʱ��S��![]() ��t��3t��
��t��3t��![]() ��
��
��10<t��20ʱ��S��![]() ��10��30��30��t��10����30t��150��
��10��30��30��t��10����30t��150��
��20<t��35ʱ��S��![]() ��10��30��10��30����t��20����30��
��10��30��10��30����t��20����30��![]() ����t��20����2��t��20����
����t��20����2��t��20����![]() ��
��
���Ͽ�֪�� 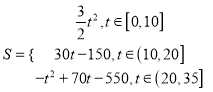 ��
��
��3����Ϊ��t��[0��10]ʱ��Smax��![]() ��102��150<650��
��102��150<650��
��t����10��20]ʱ��Smax��30��20��150��450<650��
���Ե�t����20��35]ʱ����![]() �����
�����![]() ����Ϊ20<t��35������t��30��
����Ϊ20<t��35������t��30��
��ɳ��������30 h����Ϯ��N�ǣ�

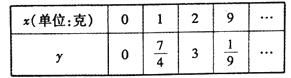
����Ŀ���������ij�豸��ʹ������![]() ���꣩����֧����ά����
���꣩����֧����ά����![]() ����Ԫ��������ͳ�����ϣ�
����Ԫ��������ͳ�����ϣ�
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
��������֪�� ![]() ��
��![]() ��������ع�ϵ������
��������ع�ϵ������
��1���ع�ֱ�߷��̣�
��2������ʹ������Ϊ10��ʱ��ά����Լ�Ƕ��٣�
�ο���ʽ���ع�ֱ�߷��̣� ![]() .����
.����
��ע�� ![]() )
)