题目内容
【题目】在平面直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系.已知点P的极坐标为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (α为参数).
(α为参数).
(1)写出点P的直角坐标及曲线C的直角坐标方程;
(2)若Q为曲线C上的动点,求PQ中点M到直线l:ρcos θ+2ρsin θ+1=0距离的最小值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据参数方程转化为直角坐标的公式得到曲线的直角坐标方程;(2)用参数形式表示出点Q的坐标,根据点到直线的距离写出表达式,由化一公式求得最值.
解析:
(1)由x=ρcos θ,y=ρsin θ可得点P的直角坐标为(3,![]() ),由
),由![]() (α为参数)
(α为参数)
得x2+(y+![]() )2=4,
)2=4,
∴曲线C的直角坐标方程为x2+(y+![]() )2=4.
)2=4.
(2)直线l的普通方程为x+2y+1=0,
曲线C的参数方程为![]() (α为参数),
(α为参数),
设Q(2cos α,-![]() +2sin α),则M
+2sin α),则M![]() ,
,
故点M到直线l的距离
d= =
=
≥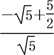 =
=![]() -1
-1![]() ,
,
∴点M到直线l的距离的最小值为![]() -1.
-1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目