题目内容
(本小题12分)已知数列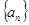 有
有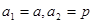 (常数
(常数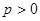 ),对任意的正整数
),对任意的正整数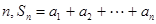 ,并有
,并有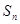 满足
满足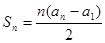 。
。
(Ⅰ)求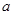 的值并证明数列
的值并证明数列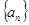 为等差数列;
为等差数列;
(Ⅱ)令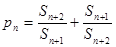 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式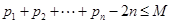 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。
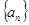 有
有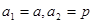 (常数
(常数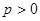 ),对任意的正整数
),对任意的正整数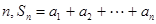 ,并有
,并有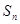 满足
满足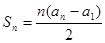 。
。(Ⅰ)求
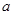 的值并证明数列
的值并证明数列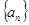 为等差数列;
为等差数列;(Ⅱ)令
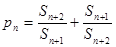 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式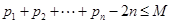 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。解:(Ⅰ)见解析;
(Ⅱ)存在最小的正整数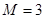 ,使不等式
,使不等式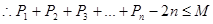 恒成立。
恒成立。
(Ⅱ)存在最小的正整数
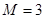 ,使不等式
,使不等式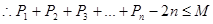 恒成立。
恒成立。本试题主要是证明等差数列和数列求和的综合运用问题。
(1)利用 ,得到
,得到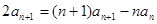
从而构造关系式得到 命题得证。
命题得证。
(2) 然后分析结构特点,得到和式,然后可以得证。
然后分析结构特点,得到和式,然后可以得证。
解:(Ⅰ)由已知,得 ……….2分
……….2分
由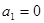 得
得 ,则
,则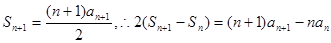
即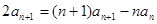 ,于是有
,于是有 ,并且
,并且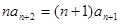 ,
,
 ,即
,即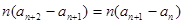
则有 ,
,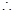
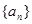 为等差数列;…….7分
为等差数列;…….7分
(Ⅱ)
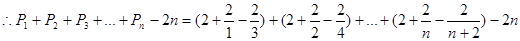
 ;由
;由 是整数可得
是整数可得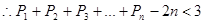 ,故存在最小的正整数
,故存在最小的正整数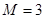 ,使不等式
,使不等式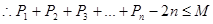 恒成立…. …. ….12分
恒成立…. …. ….12分
(1)利用
 ,得到
,得到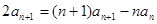
从而构造关系式得到
 命题得证。
命题得证。(2)
 然后分析结构特点,得到和式,然后可以得证。
然后分析结构特点,得到和式,然后可以得证。解:(Ⅰ)由已知,得
 ……….2分
……….2分由
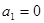 得
得 ,则
,则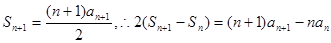
即
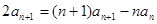 ,于是有
,于是有 ,并且
,并且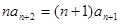 ,
, ,即
,即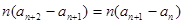
则有
 ,
,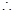
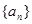 为等差数列;…….7分
为等差数列;…….7分(Ⅱ)

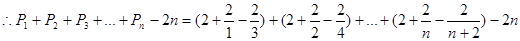
 ;由
;由 是整数可得
是整数可得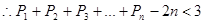 ,故存在最小的正整数
,故存在最小的正整数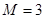 ,使不等式
,使不等式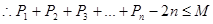 恒成立…. …. ….12分
恒成立…. …. ….12分
练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
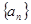 的前
的前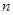 项和为
项和为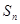 ,且满足
,且满足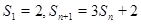
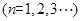 .
.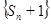 为等比数列;
为等比数列;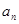 ;
;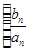 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列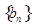 的前
的前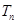 .
. 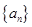 是公差为
是公差为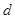 的等差数列,
的等差数列,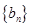 是公比为
是公比为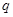 的等比数列.
的等比数列.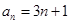 ,是否存在
,是否存在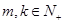 ,有
,有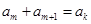 ?请说明理由;
?请说明理由;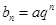 (
(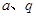 为常数,且
为常数,且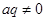 ),对任意
),对任意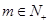 ,存在
,存在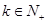 ,有
,有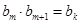 ,试求
,试求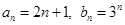 ,试确定所有的
,试确定所有的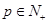 ,使数列
,使数列 项的和为数列中
项的和为数列中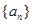 为等比数列,其前
为等比数列,其前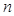 项和为
项和为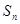 ,已知
,已知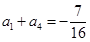 ,且对于任意的
,且对于任意的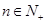 有
有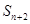 ,
,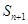 成等差;
成等差;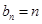 (
(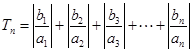 ,若
,若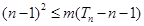 对于
对于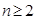 恒成立,求实数
恒成立,求实数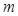 的范围.
的范围.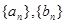 中,
中,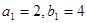 ,且
,且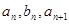 成等差数列,
成等差数列,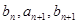 成等比数列
成等比数列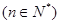 。
。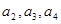 及
及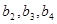 ,由此猜测
,由此猜测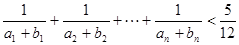 。
。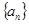 的公差
的公差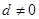 ,它的前n项和为
,它的前n项和为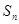 ,若
,若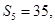 且
且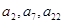 成等比数列.
成等比数列.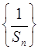 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.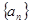 中,
中,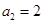 ,
,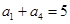 ,
,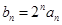 ,求数列
,求数列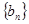 的前
的前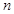 项和
项和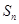 .
.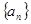 的前
的前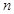 项和分别为
项和分别为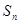 ,若
,若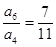 ,则
,则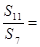 ( )
( )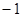

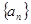 的前
的前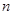 项和
项和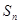 满足:对于任意
满足:对于任意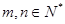 ,都有
,都有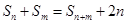 ;若
;若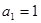 ,则
,则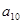 = .
= .