题目内容
已知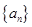 是公差为
是公差为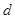 的等差数列,
的等差数列,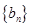 是公比为
是公比为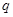 的等比数列.
的等比数列.
(Ⅰ)若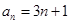 ,是否存在
,是否存在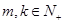 ,有
,有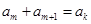 ?请说明理由;
?请说明理由;
(Ⅱ)若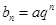 (
(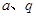 为常数,且
为常数,且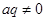 ),对任意
),对任意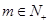 ,存在
,存在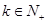 ,有
,有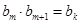 ,试求
,试求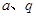 满足的充要条件;
满足的充要条件;
(Ⅲ)若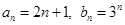 ,试确定所有的
,试确定所有的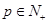 ,使数列
,使数列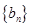 中存在某个连续
中存在某个连续 项的和为数列中
项的和为数列中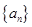 的某一项,请证明.
的某一项,请证明.
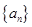 是公差为
是公差为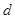 的等差数列,
的等差数列,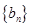 是公比为
是公比为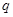 的等比数列.
的等比数列.(Ⅰ)若
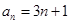 ,是否存在
,是否存在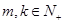 ,有
,有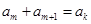 ?请说明理由;
?请说明理由;(Ⅱ)若
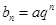 (
(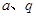 为常数,且
为常数,且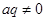 ),对任意
),对任意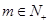 ,存在
,存在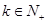 ,有
,有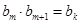 ,试求
,试求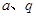 满足的充要条件;
满足的充要条件;(Ⅲ)若
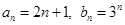 ,试确定所有的
,试确定所有的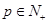 ,使数列
,使数列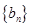 中存在某个连续
中存在某个连续 项的和为数列中
项的和为数列中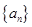 的某一项,请证明.
的某一项,请证明.(1)不存在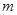 、
、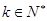 ,使等式成立。(2)
,使等式成立。(2) 、
、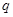 满足的充要条件是
满足的充要条件是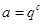 ,其中
,其中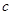 是大于等于
是大于等于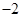 的整数 (3)见解析
的整数 (3)见解析
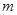 、
、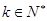 ,使等式成立。(2)
,使等式成立。(2) 、
、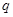 满足的充要条件是
满足的充要条件是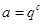 ,其中
,其中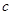 是大于等于
是大于等于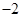 的整数 (3)见解析
的整数 (3)见解析(1)把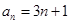 代入
代入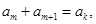 整理得
整理得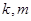 的关系,分析
的关系,分析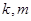 均为整数时,等式不成立,可得结论;(2)从特殊入手,先找到
均为整数时,等式不成立,可得结论;(2)从特殊入手,先找到 与
与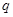 的关系,再对一般的给出证明;(3)由等比数列的求和公式求出数列
的关系,再对一般的给出证明;(3)由等比数列的求和公式求出数列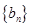 中存在某个连续
中存在某个连续 项的和,令
项的和,令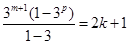 ,分析
,分析 为奇数与偶数,利用二项式定理整理
为奇数与偶数,利用二项式定理整理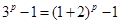 得到
得到 为奇数时满足条件
为奇数时满足条件
(1)由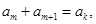 得
得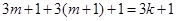 ,整理后,可得
,整理后,可得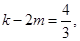
 、
、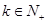 ,
,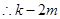 为整数
为整数 不存在
不存在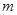 、
、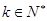 ,使等式成立。………………4分
,使等式成立。………………4分
(2)当 时,则
时,则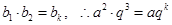 ,
,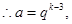 即
即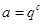 ,其中
,其中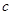 是大于等于
是大于等于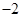 的整数反之当
的整数反之当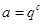 时,其中
时,其中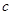 是大于等于
是大于等于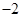 的整数,则
的整数,则 ,
,
显然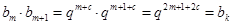 ,其中
,其中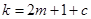

 、
、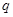 满足的充要条件是
满足的充要条件是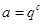 ,其中
,其中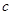 是大于等于
是大于等于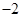 的整数……………………9分
的整数……………………9分
(3)设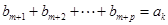 ,即
,即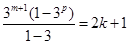 ,
,
整理得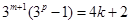
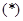
当 为偶数时,
为偶数时,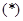 式左边为4的倍数,右边仅为2的倍数,故当
式左边为4的倍数,右边仅为2的倍数,故当 为偶数时,结论不成立。
为偶数时,结论不成立。
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,
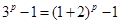

 由
由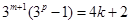 ,得
,得
 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有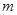 和
和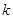 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立。
为奇数时,命题都成立。
另解:设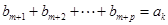
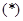 ,
,
由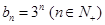 为奇数,
为奇数,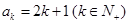 为大于等于3的奇数。
为大于等于3的奇数。
当 为偶数时,
为偶数时,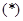 式左边=
式左边= =偶数,
=偶数,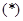 式右边=
式右边=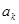 =奇数,此时矛盾;
=奇数,此时矛盾;
当 为奇数时,
为奇数时,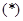 式左边=
式左边= =奇数,所以存在满足条件的
=奇数,所以存在满足条件的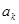 ,使得
,使得
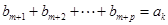 成立。
成立。
综上所述, 为奇数时,满足条件
为奇数时,满足条件
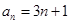 代入
代入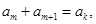 整理得
整理得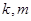 的关系,分析
的关系,分析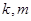 均为整数时,等式不成立,可得结论;(2)从特殊入手,先找到
均为整数时,等式不成立,可得结论;(2)从特殊入手,先找到 与
与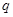 的关系,再对一般的给出证明;(3)由等比数列的求和公式求出数列
的关系,再对一般的给出证明;(3)由等比数列的求和公式求出数列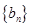 中存在某个连续
中存在某个连续 项的和,令
项的和,令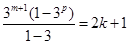 ,分析
,分析 为奇数与偶数,利用二项式定理整理
为奇数与偶数,利用二项式定理整理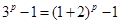 得到
得到 为奇数时满足条件
为奇数时满足条件(1)由
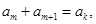 得
得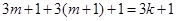 ,整理后,可得
,整理后,可得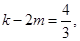
 、
、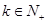 ,
,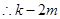 为整数
为整数 不存在
不存在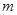 、
、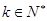 ,使等式成立。………………4分
,使等式成立。………………4分(2)当
 时,则
时,则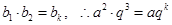 ,
,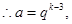 即
即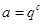 ,其中
,其中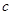 是大于等于
是大于等于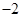 的整数反之当
的整数反之当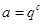 时,其中
时,其中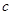 是大于等于
是大于等于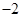 的整数,则
的整数,则 ,
,显然
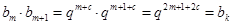 ,其中
,其中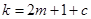

 、
、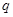 满足的充要条件是
满足的充要条件是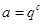 ,其中
,其中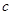 是大于等于
是大于等于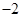 的整数……………………9分
的整数……………………9分(3)设
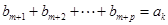 ,即
,即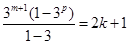 ,
,整理得
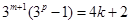
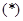
当
 为偶数时,
为偶数时,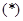 式左边为4的倍数,右边仅为2的倍数,故当
式左边为4的倍数,右边仅为2的倍数,故当 为偶数时,结论不成立。
为偶数时,结论不成立。当
 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,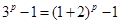

 由
由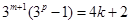 ,得
,得
 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有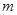 和
和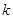 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立。
为奇数时,命题都成立。另解:设
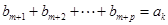
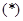 ,
,由
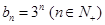 为奇数,
为奇数,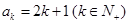 为大于等于3的奇数。
为大于等于3的奇数。当
 为偶数时,
为偶数时,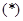 式左边=
式左边= =偶数,
=偶数,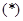 式右边=
式右边=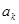 =奇数,此时矛盾;
=奇数,此时矛盾;当
 为奇数时,
为奇数时,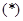 式左边=
式左边= =奇数,所以存在满足条件的
=奇数,所以存在满足条件的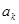 ,使得
,使得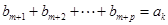 成立。
成立。综上所述,
 为奇数时,满足条件
为奇数时,满足条件
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
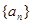 ,其前
,其前 项和为
项和为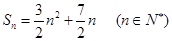 .
.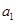 ,
,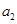 ;
;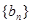 满足
满足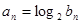 ,请证明数列
,请证明数列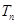 .
.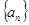 有
有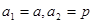 (常数
(常数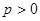 ),对任意的正整数
),对任意的正整数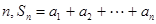 ,并有
,并有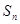 满足
满足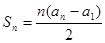 。
。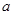 的值并证明数列
的值并证明数列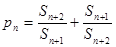 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式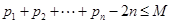 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。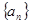 的前
的前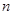 项和为
项和为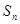 ,等比数列
,等比数列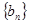 的前
的前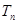 ,它们满足
,它们满足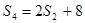 ,
,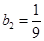 ,
,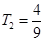 ,且当
,且当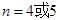 时,
时,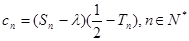 ,如果
,如果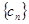 是单调数列,求实数
是单调数列,求实数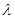 的取值范围.
的取值范围.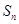 是数列
是数列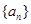 的前
的前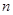 项和,且
项和,且
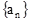 的通项公式;
的通项公式; 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列 (n为正整数),求数列
(n为正整数),求数列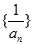 的前
的前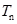 ,若
,若 对
对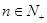 恒成立,求正整数
恒成立,求正整数 的最小值。
的最小值。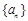 的前n项和为
的前n项和为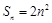 ,
,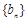 为等比数列,且
为等比数列,且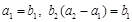 .
.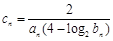 ,求数列
,求数列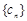 的前n项和
的前n项和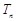 .
. 的前n项和为bn,数列
的前n项和为bn,数列 的前n项积为cn且
的前n项积为cn且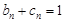 ,则数列
,则数列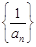 中最接近2012的数是( )
中最接近2012的数是( )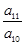 <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为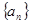 中,若
中,若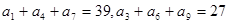 ,则数列的前9项的
,则数列的前9项的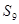 等于______.
等于______.