题目内容
设数列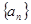 的前
的前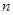 项和为
项和为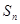 ,且满足
,且满足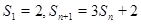
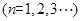 .
.
(Ⅰ)求证:数列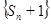 为等比数列;
为等比数列;
(Ⅱ)求通项公式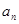 ;
;
(Ⅲ)若数列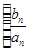 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列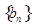 的前
的前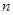 项和为
项和为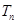 .
.
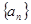 的前
的前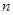 项和为
项和为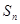 ,且满足
,且满足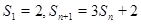
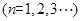 .
.(Ⅰ)求证:数列
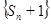 为等比数列;
为等比数列;(Ⅱ)求通项公式
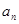 ;
;(Ⅲ)若数列
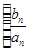 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列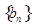 的前
的前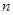 项和为
项和为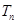 .
. (Ⅰ)见解析 (Ⅱ)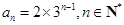 . (Ⅲ)
. (Ⅲ)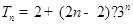 .
.
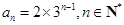 . (Ⅲ)
. (Ⅲ)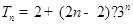 .
.(I)根据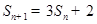 ,可得
,可得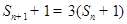 ,
,
从而可证明: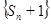 为等比数列.
为等比数列.
(II)在(I)的基础上先求出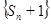 的通项公式,然后再根据Sn求出an.
的通项公式,然后再根据Sn求出an.
(III)先求出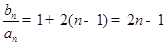 ,
,
再根据an的通项公式求出bn,由于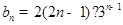 ,所以易采用错位相减的方法求和
,所以易采用错位相减的方法求和
证明:(Ⅰ)因为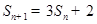 ,所以
,所以 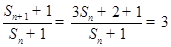 . 又
. 又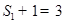 ,
,
所以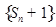 是首项为
是首项为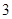 ,公比为
,公比为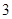 的等比数列.
的等比数列.
(Ⅱ)由(Ⅰ)可得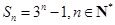 .当
.当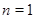 时,
时,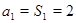 .
.
当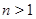 时,
时,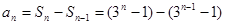
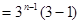
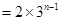 .
.
故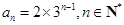 .
.
(Ⅲ)因为 数列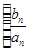 是首项为1,公差为2的等差数列,所以
是首项为1,公差为2的等差数列,所以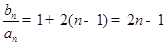 .所以
.所以 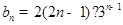 .
.
所以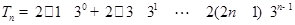 .
.
所以 .
.
所以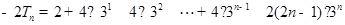
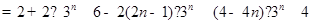 .
.
所以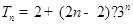 .
.
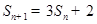 ,可得
,可得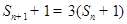 ,
,从而可证明:
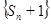 为等比数列.
为等比数列.(II)在(I)的基础上先求出
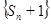 的通项公式,然后再根据Sn求出an.
的通项公式,然后再根据Sn求出an.(III)先求出
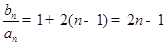 ,
,再根据an的通项公式求出bn,由于
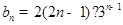 ,所以易采用错位相减的方法求和
,所以易采用错位相减的方法求和证明:(Ⅰ)因为
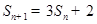 ,所以
,所以 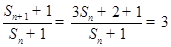 . 又
. 又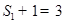 ,
,所以
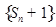 是首项为
是首项为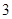 ,公比为
,公比为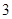 的等比数列.
的等比数列.(Ⅱ)由(Ⅰ)可得
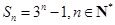 .当
.当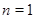 时,
时,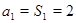 .
.当
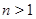 时,
时,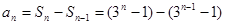
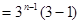
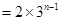 .
.故
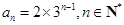 .
.(Ⅲ)因为 数列
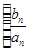 是首项为1,公差为2的等差数列,所以
是首项为1,公差为2的等差数列,所以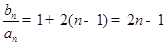 .所以
.所以 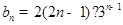 .
.所以
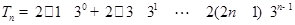 .
.所以
 .
.所以
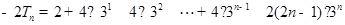
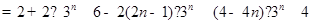 .
.所以
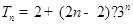 .
.
练习册系列答案
相关题目
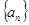 有
有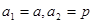 (常数
(常数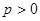 ),对任意的正整数
),对任意的正整数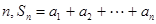 ,并有
,并有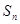 满足
满足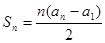 。
。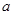 的值并证明数列
的值并证明数列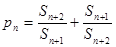 ,是否存在正整数M,使不等式
,是否存在正整数M,使不等式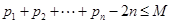 恒成立,若存在,求出M的最小值,若不存在,说明理由。
恒成立,若存在,求出M的最小值,若不存在,说明理由。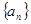 的前
的前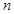 项和为
项和为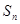 ,且
,且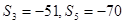 ,
,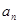 及前
及前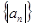 的前14项和
的前14项和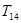 。
。 (其中常数λ>0,n∈N*).
(其中常数λ>0,n∈N*). }的前n项和为Sn,且S3 =6,则5a1+a7,的值为
}的前n项和为Sn,且S3 =6,则5a1+a7,的值为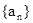 的前n项和为
的前n项和为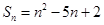 ,则数列
,则数列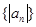 的前10项和为( )
的前10项和为( )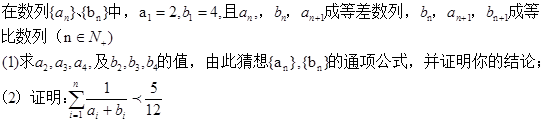
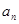 }中,
}中,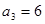 ,
,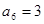 , 则通项公式
, 则通项公式