题目内容
17.原点与极点重合,x轴正半轴与极轴重合,则直角坐标为$(-2,-2\sqrt{3})$的点的极坐标是( )| A. | $(4,\frac{π}{3})$ | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | $(4,\frac{2π}{3})$ |
分析 根据极坐标公式,求出ρ、θ即可.
解答 解:∵x=-2,y=-2$\sqrt{3}$;
∴ρ=$\sqrt{{x}^{2}{+y}^{2}}$=$\sqrt{{(-2)}^{2}{+(-2\sqrt{3})}^{2}}$=4;
又x=ρcosθ=-2,∴cosθ=-$\frac{2}{ρ}$=-$\frac{1}{2}$,
且θ为第三象限角,
∴θ=$\frac{4π}{3}$;
∴该点的极坐标为(4,$\frac{4π}{3}$).
故选:B.
点评 本题考查了极坐标方程的应用问题,解题时应熟记极坐标与普通方程的互化,是基础题目.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
7.若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称,则f(x)的最大值是( )
| A. | 9 | B. | 14 | C. | 15 | D. | 16 |
5.已知集合A={x|$\frac{x}{x-1}$≥0,x∈R},B={y|y=2x+1,x∈R},则A∩B=( )
| A. | (1,+∞) | B. | (-∞,0) | C. | (0,1] | D. | [0,1] |
7.若执行如图所示的程序框图,则输出的i的值为( )
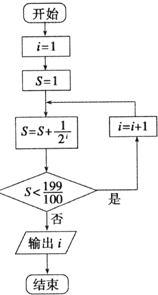

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |