题目内容
5．已知集合A={x|$\frac{x}{x-1}$≥0，x∈R}，B={y|y=2x+1，x∈R}，则A∩B=（ ）| A． | （1，+∞） | B． | （-∞，0） | C． | （0，1] | D． | [0，1] |
分析 求出A中不等式的解集确定出A，求出B中y的范围确定出B，找出A与B的交集即可．
解答 解：由A中不等式变形得：x（x-1）≥0，且x-1≠0，
解得：x≤0或x＞1，即A=（-∞，0]∪（1，+∞），
由B中y=2x+1＞1，得到B=（1，+∞），
则A∩B=（1，+∞）．
故选：A．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
全能测控一本好卷系列答案
相关题目
15．已知全集U=R，集合A={x|-2≤x＜3}，B={y|y=2x-1，x≥0}，则A∩∁UB=（ ）
| A． | {x|-2≤x＜0} | B． | $\left\{{x\left|{-2≤x＜\frac{1}{2}}\right.}\right\}$ | C． | $\left\{{x\left|{0≤x＜\frac{1}{2}}\right.}\right\}$ | D． | {x|0≤x＜3} |
20．
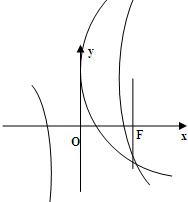如图，已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点，且两条曲线的交点的连线过F，则该双曲线的离心率为（ ）
如图，已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点，且两条曲线的交点的连线过F，则该双曲线的离心率为（ ）| A． | $\sqrt{2}$+1 | B． | 2 | C． | $\sqrt{2}$ | D． | $\sqrt{2}$-1 |
17．原点与极点重合，x轴正半轴与极轴重合，则直角坐标为$（-2，-2\sqrt{3}）$的点的极坐标是（ ）
| A． | $（4，\frac{π}{3}）$ | B． | （4，$\frac{4π}{3}$） | C． | （-4，-$\frac{2π}{3}$） | D． | $（4，\frac{2π}{3}）$ |