题目内容
8.实数x,y,k满足$\left\{\begin{array}{l}{x+y-3≥0}\\{x-y+1≥0}\\{x≤k}\end{array}\right.$,z=x2+y2,若z的最大值为13,则k的值为2.分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出不等式组对应的平面区域如图;则k>1,
则z的几何意义是区域内的点到原点的距离的平方,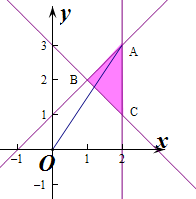
由图象知,O到A的距离最大,
∵z=x2+y2的最大值为13,
∴O到A的距离最大为d=$\sqrt{13}$,
由$\left\{\begin{array}{l}{x=k}\\{x-y+1=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x=k}\\{y=k+1}\end{array}\right.$,
即A(k,k+1),
则OA=$\sqrt{{k}^{2}+(k+1)^{2}}$=$\sqrt{13}$,
即2k2+2k+1=13,
即k2+k-6=0,解得k=2或k=-3(舍),
故k=2,
故答案为:2
点评 本题主要考查线性规划以及点到直线的距离的应用,利用数形结合是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.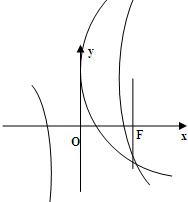 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
17.原点与极点重合,x轴正半轴与极轴重合,则直角坐标为$(-2,-2\sqrt{3})$的点的极坐标是( )
| A. | $(4,\frac{π}{3})$ | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | $(4,\frac{2π}{3})$ |
18.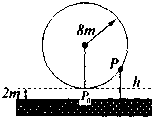 一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
 一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | h(t)=-8sin$\frac{π}{6}$t+10 | B. | h(t)=-cos$\frac{π}{6}$t+10 | C. | h(t)=-8sin$\frac{π}{6}$t+8 | D. | h(t)=-8cos$\frac{π}{6}$t+10 |