若函数f(x)=(1-x2)(x2+ax+b)的图象关于直线x=2对称.则fA．9B．14C．15D．16 题目和参考答案——青夏教育精英家教网——

题目内容

7．若函数f（x）=（1-x²）（x²+ax+b）的图象关于直线x=2对称，则f（x）的最大值是（　　）

A．

9

B．

14

C．

15

D．

16

分析根据对称性求出a，b，利用导数研究函数的最值即可．

解答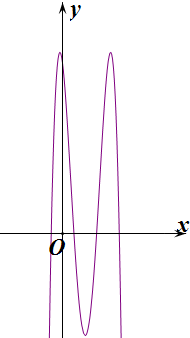解：∵f（x）=（1-x²）（x²+ax+b）的图象关于直线x=2对称，
∴f（1）=f（3），f（-1）=f（5），
即$\left\{\begin{array}{l}{9+3a+b=0}\\{25+5a+b=0}\end{array}\right.$，解得a=-8，b=15，
即f（x）=（1-x²）（x²-8x+15）=-x⁴+8x³-14x²-8x+15，
则f′（x）=-4x³+24x²-28x-8=-4（x-2）（x²-4x-1），
由f′（x）=0，解得x=2或x=2+$\sqrt{5}$或x=2-$\sqrt{5}$，
由f′（x）＞0，解得2＜x＜2+$\sqrt{5}$或x＜2-$\sqrt{5}$，此时函数单调递增，
由f′（x）＜0，解得2-$\sqrt{5}$＜x＜2或x＞2+$\sqrt{5}$，此时函数单调递减，
作出对应的函数图象如图：
则当x=2-$\sqrt{5}$或2+$\sqrt{5}$时，函数f（x）取得极大值同时也是最大值
则f（2+$\sqrt{5}$）=16，
故选：D．

点评本题主要考查函数最值的区间，根据对称性求出a，b的值，利用导数研究函数的单调性和函数的最值求法等知识，综合性较强．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

20．已知定义在R上的函数f（x）满足：（1）f（x）+f（2-x）=0，（2）f（x-2）=f（-x），（3）在[-1，1]上表达式为f（x）=$\left\{\begin{array}{l}\sqrt{1-{x^2}}，x∈[-1，0]\\ cos（\frac{π}{2}x），x∈（0，1]\end{array}$，则函数f（x）与函数g（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{1-x，x＞0}\end{array}\right.$的图象区间[-3，3]上的交点个数为（　　）

1．已知x，y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-5≤0}\\{x+y-4≥0}\end{array}\right.$．
（1）求x²+y²的最大值和最小值；
（2）求z=$\frac{y-1}{x+1}$的取值范围；
（3）求z=|x+2y-4|的取值范围．

15．已知全集U=R，集合A={x|-2≤x＜3}，B={y|y=2^x-1，x≥0}，则A∩∁_UB=（　　）

$\left\{{x\left|{-2≤x＜\frac{1}{2}}\right.}\right\}$

$\left\{{x\left|{0≤x＜\frac{1}{2}}\right.}\right\}$

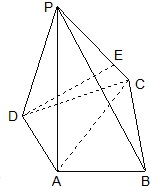如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AC⊥AB，AD⊥DC，∠DAC=60°，PA=AC=2，AB=1，点E在棱PC上，且DE⊥PB．
（Ⅰ）求CE的长；
（Ⅱ）求二面角A-PB-C的正弦值．

12．已知函数f（x）=x+$\frac{a+1}{x}$-alnx（a∈R）．
（Ⅰ）当a=1时，求曲线f（x）在x=1处的切线方程；
（Ⅱ）若在[1，e]（e=2.71828…为自然对数的底数）上存在一点x₀，使得f（x₀）≤0成立，求a的取值范围；
（Ⅲ）当a＞0时，设函数g（x）=f（ax）-$\frac{a+1}{ax}$，若g（x）有两个不同的零点x₁，x₂，且0＜x₁＜x₂，求证：$\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$＜lna．

19．函数$f（x）=\sqrt{|x+1|+|x+2|-a}$．
（1）a=5，函数f（x）的定义域A；
（2）设B={x|-1＜x＜2}，当实数a，b∈（B∩C_RA）时，证明：$\frac{|a+b|}{2}＜|1+\frac{ab}{4}|$．

16．已知函数f（x）=lnx．
（1）方程f（x+a）=x有且只有一个实数解，求a的值；
（2）若函数$g（x）=f（x）+\frac{1}{2}{x^2}-mx（m≥\frac{5}{2}）$的极值点x₁，x₂（x₁＜x₂）恰好是函数h（x）=f（x）-cx²-bx的零点，求$y=（{x_1}-{x_2}）h'（\frac{{{x_1}+{x_2}}}{2}）$的最小值．

17．原点与极点重合，x轴正半轴与极轴重合，则直角坐标为$（-2，-2\sqrt{3}）$的点的极坐标是（　　）

$（4，\frac{π}{3}）$

（4，$\frac{4π}{3}$）

（-4，-$\frac{2π}{3}$）

$（4，\frac{2π}{3}）$