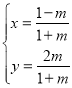题目内容
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是线段
分别是线段![]() 与
与![]() 上的点,则与平面
上的点,则与平面![]() 平行的直线
平行的直线![]() 有( )
有( )
A.0条B.1条C.2条D.无数条
【答案】D
【解析】
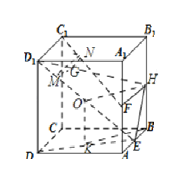
取![]() 的中点
的中点![]() ,连接
,连接![]() ,在
,在![]() 上任取一点
上任取一点![]() ,过
,过![]() 在面
在面![]() 中,作
中,作![]() 平行于
平行于![]() ,其中
,其中![]() 为线段
为线段![]() 的中点,交
的中点,交![]() 于
于![]() ,再过
,再过![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,根据线面平行的判定定理,得到
,根据线面平行的判定定理,得到![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再根据面面平行的判断定理得到平面
,再根据面面平行的判断定理得到平面![]() 平面
平面![]() ,由面面平行的性质得到则
,由面面平行的性质得到则![]() 平面
平面![]() ,由于
,由于![]() 是任意的,故
是任意的,故![]() 有无数条.
有无数条.
如图:
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
连接![]() ,在
,在![]() 上任取一点
上任取一点![]() ,
,
过![]() 在面
在面![]() 中,作
中,作![]() 平行于
平行于![]() ,
,
其中![]() 为线段
为线段![]() 的中点,交
的中点,交![]() 于
于![]() ,
,
再过![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
![]() 在平面
在平面![]() 的正投影为
的正投影为![]() ,连接
,连接![]() ,则
,则![]() ,
,
由于![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
同理由![]() ,可推得
,可推得![]() 平面
平面![]() ,
,
由面面平行的判定定理得,平面![]() 平面
平面![]() ,
,
则![]() 平面
平面![]() .
.
由于![]() 为
为![]() 上任一点,故这样的直线
上任一点,故这样的直线![]() 有无数条.
有无数条.
故选:![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目