题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为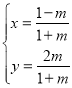 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() 点,若
点,若![]() ,求
,求![]() .
.
【答案】(1)![]() 的普通方程为
的普通方程为![]() ;
;![]() 的直角方程为
的直角方程为![]() ; (2)
; (2)![]()
【解析】
(1)根据加减消元得曲线![]() 的普通方程,根据
的普通方程,根据![]() ,
,![]() 得
得![]() 的直角坐标方程;
的直角坐标方程;
(2)先写出直线![]() ,
,![]() 参数方程,代入
参数方程,代入![]() ,
,![]() ,再根据参数几何意义化简条件解得结果.
,再根据参数几何意义化简条件解得结果.
(1)①:∵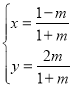 (
(![]() 为参数),∴
为参数),∴![]() ,
,
又∵![]() ,
,
∴曲线![]() 的普通方程为
的普通方程为![]() ;
;
②∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴曲线![]() 的直角方程为
的直角方程为![]() ;
;
(2)由题意,设![]() (
(![]() 为参数),
为参数),![]() (
(![]() 为参数),
为参数),
依题意,![]() ,
,
![]() 与
与![]() 联立得
联立得![]() ,
,
![]() 与
与![]() 联立得
联立得![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,则
,则
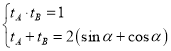 ,
,![]() ,
,
由![]() 且
且![]() ,得
,得![]() .
.
∴![]() ,即
,即![]() ,故
,故![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中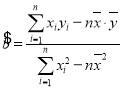 .参考数据:
.参考数据:![]() ,
,![]() )
)