题目内容
(本小题满分12分) 已知正三棱锥的的侧面积为
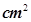 ,高为
,高为 ,
,
求它的体积。

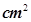 ,高为
,高为 ,
,求它的体积。
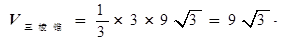
先通过侧面积求出侧面的斜高,再利用勾股定理求出底面边长,从而利用体积公式即可求解三棱锥的体积
解:设正三棱锥的度面边长为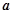 ,斜高为
,斜高为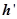 ,底面内切圆半径为
,底面内切圆半径为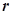 。
。

 ………………2分
………………2分
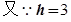 ,
,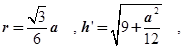 ………………4分
………………4分
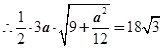 得
得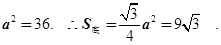 …………10分
…………10分
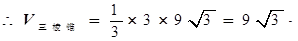 ………………12分
………………12分
解:设正三棱锥的度面边长为
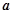 ,斜高为
,斜高为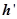 ,底面内切圆半径为
,底面内切圆半径为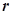 。
。
 ………………2分
………………2分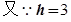 ,
,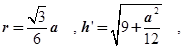 ………………4分
………………4分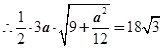 得
得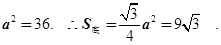 …………10分
…………10分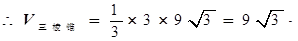 ………………12分
………………12分
练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
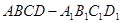 的棱长为
的棱长为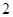 ,
,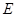 为
为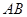 的中点.
的中点.
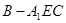 的体积;
的体积;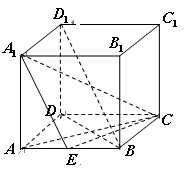
 ,类比以上结论,则长、宽、高分别为
,类比以上结论,则长、宽、高分别为 的长方体的外接球半径为( )
的长方体的外接球半径为( )



 的正三棱柱外接球的体积为
的正三棱柱外接球的体积为 ,则该三棱柱的体积为
,则该三棱柱的体积为  中,
中, ,
, ,则四棱锥
,则四棱锥 的体积为 ▲ cm3.
的体积为 ▲ cm3.
 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .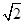 ,则此球的体积为( )
,则此球的体积为( )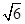 π
π π
π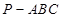 的四个顶点都在体积为
的四个顶点都在体积为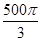 的球的表面上,平面
的球的表面上,平面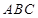 所在的小圆面积为
所在的小圆面积为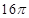 ,则该三棱锥的高的最大值是
,则该三棱锥的高的最大值是