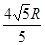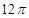题目内容
将一个长和宽分别为 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .
 的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则
的长方形的四个角切去四个相同的正方形,然后折成一个无盖的长方体形的盒子,若这个长方体的外接球的体积存在最小值,则 的取值范围是 .
的取值范围是 .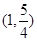 .
. 设正方形的边长为x,则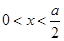 ,则此长方体的外接球直径最小时,其外接球的体积存在最小值.
,则此长方体的外接球直径最小时,其外接球的体积存在最小值.
由于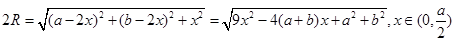
当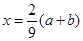 时,2R才存在最小值,因为0<a<b,所以
时,2R才存在最小值,因为0<a<b,所以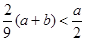 ,所以
,所以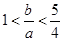
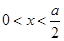 ,则此长方体的外接球直径最小时,其外接球的体积存在最小值.
,则此长方体的外接球直径最小时,其外接球的体积存在最小值.由于
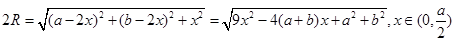
当
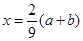 时,2R才存在最小值,因为0<a<b,所以
时,2R才存在最小值,因为0<a<b,所以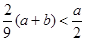 ,所以
,所以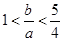

练习册系列答案
相关题目
 中,四边形
中,四边形 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
. ;
; 为线段
为线段 的中点,求证:
的中点,求证: ;
; ,且二面角
,且二面角 的大小为
的大小为 ,
, 的体积.
的体积. 

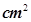 ,高为
,高为 ,
, 中,平面
中,平面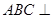 平面
平面 ,
,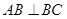 ,
,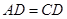 ,
,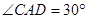 。
。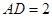 ,
, ,求四面体
,求四面体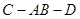 为
为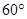 ,求异面直线
,求异面直线 与
与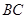 所成角的余弦值。(12分)
所成角的余弦值。(12分)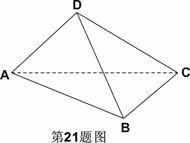
 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积. 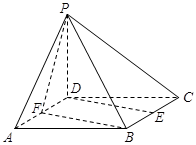
 ,则这两地的球面距离是( ).
,则这两地的球面距离是( ). 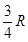
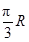

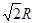
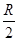 和
和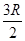
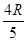 和
和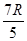
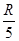 和
和
 和
和