题目内容
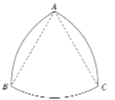
【题目】勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线,它由德国机械工程专家,机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形,现在勒洛三角形中随机取一点,则此点取自正三角形外的概率为( )
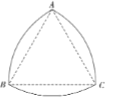
A.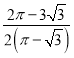 B.
B.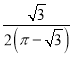
C.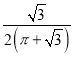 D.
D.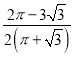
【答案】A
【解析】
设![]() ,将圆心角为
,将圆心角为![]() 的扇形面积减去等边三角形的面积可得出弓形的面积,由此计算出图中“勒洛三角形”的面积,然后利用几何概型的概率公式可计算出所求事件的概率.
的扇形面积减去等边三角形的面积可得出弓形的面积,由此计算出图中“勒洛三角形”的面积,然后利用几何概型的概率公式可计算出所求事件的概率.
如下图所示,设![]() ,则以点
,则以点![]() 为圆心的扇形面积为
为圆心的扇形面积为![]() ,
,
等边![]() 的面积为
的面积为![]() ,其中一个弓形的面积为
,其中一个弓形的面积为![]() ,
,
所以,勒洛三角形的面积可视为一个扇形面积加上两个弓形的面积,
即![]() ,
,
![]() 在勒洛三角形中随机取一点,此点取自正三角形外部的概率
在勒洛三角形中随机取一点,此点取自正三角形外部的概率 ,故选:A.
,故选:A.

【题目】为考查某种药物预防疾病的效果,随机抽查了50只服用药的动物和50只未服用药的动得知服用药的动物中患病的比例是![]() ,未服用药的动物中患病的比例为
,未服用药的动物中患病的比例为![]() .
.
(I)根据以上数据完成下列2×2列联表:
患病 | 未患病 | 总计 | |
服用药 | |||
没服用药 | |||
总计 |
(II)能否有99%的把握认为药物有效?并说明理由.
附:
| … | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| … | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |

【题目】手机支付也称为移动支付,是指允许用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.随着信息技术的发展,手机支付越来越成为人们喜欢的支付方式.某机构对某地区年龄在15到75岁的人群“是否使用手机支付”的情况进行了调查,随机抽取了100人,其年龄频率分布表和使用手机支付的人数如下所示:(年龄单位:岁)
年龄段 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频率 | 0.1 | 0.32 | 0.28 | 0.22 | 0.05 | 0.03 |
使用人数 | 8 | 28 | 24 | 12 | 2 | 1 |
(1)若以45岁为分界点,根据以上统计数据填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为“使用手机支付”与年龄有关?
年龄低于45岁 | 年龄不低于45岁 | |
使用手机支付 | ||
不使用手机支付 |
(2)若从年龄在[55,65),[65,75]的样本中各随机选取2人进行座谈,记选中的4人中“使用手机支付”的人数为X,求随机变量X的分布列和数学期望.
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.