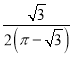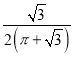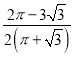题目内容
【题目】已知定义在R上的函数
满足
，且
为偶函数，若在
内单调递减，则下面结论正确的是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
由题意可判断函数f（x）的周期为6，对称轴为x＝3，所以有f（12.5）＝f（0.5），f（-4.5）＝f（1.5），f（3.5）＝f（2.5），因为0＜0.5＜1.5＜2.5＜3，且函数在（0，3）内单调递减，从而判断大小
∵函数
满足
，∴
=
，
∴f（x）在R上是以6为周期的函数，∴f（12.5）＝f（12+0.5）＝f（0.5），
又
为偶函数，∴f（x）的对称轴为x＝3，∴f（3.5）＝f（2.5），
又∵0＜0.5＜1.5＜2.5＜3，
且在（0，3）内单调递减，∴f（2.5）＜f（1.5）＜f（0.5）
即f（3.5）＜f（-4.5）＜f（12.5）
故选：B．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
【题目】某中学拟在高一下学期开设游泳选修课，为了了解高一学生喜欢游泳是否与性别有关，现从高一学生中抽取100人做调查，得到
列联表：
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在100个人中随机抽取1人，抽到喜欢游泳的学生的概率为
．
（1）请完成上面的列联表；
（2）根据列联表的数据，是否有99.9%的把握认为喜欢游泳与性别有关？并说明你的理由．
参考公式与临界值表：
．
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
