题目内容
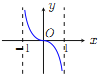
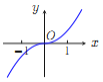
【题目】已知函数![]() .
.
(Ⅰ)求方程![]() 的实数解;
的实数解;
(Ⅱ)如果数列![]() 满足
满足![]() ,
,![]() (
(![]() ),是否存在实数
),是否存在实数![]() ,使得
,使得![]() 对所有的
对所有的![]() 都成立?证明你的结论.
都成立?证明你的结论.
(Ⅲ)在(Ⅱ)的条件下,设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)存在
;(Ⅱ)存在![]() 使得
使得![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】(Ⅰ)由题意,通过解分式方程即可得方程的实数解析;(Ⅱ)通过函数![]() 的单调性判断数列通项
的单调性判断数列通项![]() 的范围,再利用数学归纳法进行证明;(Ⅲ)由(Ⅱ)可得通项
的范围,再利用数学归纳法进行证明;(Ⅲ)由(Ⅱ)可得通项![]() 的范围,构造新数列
的范围,构造新数列![]() ,通过计算数列
,通过计算数列![]() 的前
的前![]() 和及其范围,再利用数学归纳法证明之.
和及其范围,再利用数学归纳法证明之.
试题解析:(Ⅰ)![]() ;
;
(Ⅱ)存在![]() 使得
使得![]() .
.
证法1:因为![]() ,当
,当![]() 时,
时,![]() 单调递减,所以
单调递减,所以![]() .因为
.因为![]() ,所以由
,所以由![]() 得
得![]() 且
且![]() .下面用数学归纳法证明
.下面用数学归纳法证明![]() .
.
因为![]() ,所以当
,所以当![]() 时结论成立.
时结论成立.
假设当![]() 时结论成立,即
时结论成立,即![]() .由于
.由于![]() 为
为![]() 上的减函数,所以
上的减函数,所以![]() ,从而
,从而![]() ,
,
因此![]() ,
,
即![]() .
.
综上所述,对一切![]() ,
,![]() 都成立,
都成立,
即存在![]() 使得
使得![]() .
.
证法2: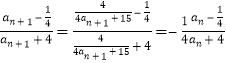 ,且
,且![]()
![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
所以![]() .
.
易知![]() ,所以当
,所以当![]() 为奇数时,
为奇数时,![]() ;当
;当![]() 为偶数时,
为偶数时,![]()
即存在![]() ,使得
,使得![]() .
.
(Ⅲ)证明:由(2),我们有![]() ,从而
,从而![]() .
.
设![]() ,则由
,则由![]() 得
得![]() .
.
由于![]() ,
,
因此n=1,2,3时,![]() 成立,左边不等式均成立.
成立,左边不等式均成立.
当n>3时,有 ,
,
因此![]() .
.
从而![]() .即
.即![]() .
.
解法2: 由(Ⅱ)可知![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
所以![]()
所以当![]() 为偶数时,
为偶数时,![]() ;所以当
;所以当![]() 为奇数时,
为奇数时,![]()
即![]() .(其他解法酌情给分)
.(其他解法酌情给分)

【题目】某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
专业A | 专业B | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=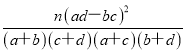
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某电视台在一次对收看文艺节目和新闻节目的抽样调查中,随机抽取了100名电视观众,相关的数据如表所示:
类别 | 文艺节目 | 新闻节目 | 总计 |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,则大于40岁的观众应该抽取几名?