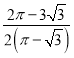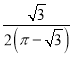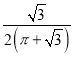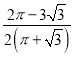题目内容
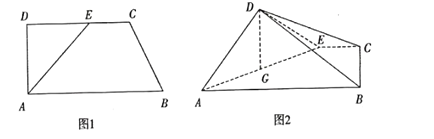
【题目】如图,四面体![]() 中,
中,![]() 是正三角形,
是正三角形,![]() 是直角三角形,
是直角三角形,![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为
为![]() 中点,求二面角
中点,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先证明出![]() ,可得出
,可得出![]() ,可得出
,可得出![]() ,然后取
,然后取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,并设
,并设![]() ,利用勾股定理证明出
,利用勾股定理证明出![]() ,由等腰三角形三线合一得出
,由等腰三角形三线合一得出![]() ,利用直线与平面垂直的判定定理可证明出
,利用直线与平面垂直的判定定理可证明出![]() 平面
平面![]() ,再利用平面与平面垂直的判定定理可得出平面
,再利用平面与平面垂直的判定定理可得出平面![]() 平面
平面![]() ;
;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,计算出平面
,计算出平面![]() 和
和![]() 的法向量,利用空间向量法求出二面角
的法向量,利用空间向量法求出二面角![]() 的余弦值,再利用同角三角函数的基本关系可得出答案.
的余弦值,再利用同角三角函数的基本关系可得出答案.
(1)![]() 是等边三角形,
是等边三角形,![]() ,又
,又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 为直角三角形,所以
为直角三角形,所以![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
设![]() ,则
,则![]() ,又
,又![]() ,
,
![]() ,
,![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,因此,平面
,因此,平面![]() 平面
平面![]() ;
;
(2)由题设及(1)可知![]() 、
、![]() 、
、![]() 两两垂直,以点
两两垂直,以点![]() 为坐标原点,建立如下图所示的空间直角坐标系
为坐标原点,建立如下图所示的空间直角坐标系![]() ,设
,设![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 的中点,则
的中点,则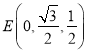 ,
,
![]() ,
,![]() ,
,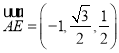 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,由
,由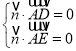 ,得
,得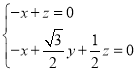 ,
,
得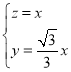 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
所以,平面![]() 的一个法向量为
的一个法向量为![]() .
.
同理可得,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
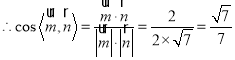 ,
,
所以,二面角![]() 的正弦值为
的正弦值为 .
.

【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由.
参考公式与临界值表:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】我们知道,地球上的水资源有限,爱护地球、节约用水是我们每个人的义务与责任.某市政府为了对自来水的使用进行科学管理,节约水资源,计划确定一个家庭年用水量的标准.为此,对全市家庭日常用水量的情况进行抽样抽查,获得了![]() 个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
个家庭某年的用水量(单位:立方米),统计结果如下表及图所示.
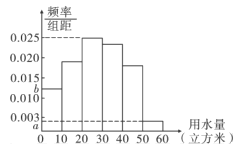
分组 | 频数 | 频率 |
| 25 | |
| 0.19 | |
| 50 | |
| 0.23 | |
| 0.18 | |
| 5 |
(1)分别求出![]() ,
,![]() 的值;
的值;
(2)若以各组区间中点值代表该组的取值,试估计全市家庭年均用水量;
(3)从样本中年用水量在![]() (单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
(单位:立方米)的5个家庭中任选3个,作进一步的跟踪研究,求年用水量最多的家庭被选中的概率(5个家庭的年用水量都不相等).
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)在答题卡上画出这些数据的频率分布直方图(要求用阴影部分显示);
(2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
(3)估计这种产品质量指标值的平均值及中位数(其中求平均值时同一组中的数据用该组区间的中点值作代表,求中位数精确到0.1).