题目内容
18.函数y=cos2(x+$\frac{π}{2}$)的单调递增区间( )| A. | (kπ,kπ+$\frac{π}{2}$)k∈Z | B. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z | C. | (2kπ,2kπ+π)k∈Z | D. | (2kπ,2kπ+2π)k∈Z |
分析 函数y=cos2(x+$\frac{π}{2}$)=$\frac{1-cos2x}{2}$ 的单调递增区间,即函数t=cos2x的减区间.再根据余弦函数的减区间求得故函数t的减区间.
解答 解:函数y=cos2(x+$\frac{π}{2}$)=sin2x=$\frac{1-cos2x}{2}$ 的单调递增区间,即函数t=cos2x的减区间.
令 2kπ≤2x≤2kπ+π,k∈z,求得kπ≤x≤kπ+$\frac{π}{2}$,故函数t的减区间为[kπ,kπ+$\frac{π}{2}$],k∈z,
故选:A.
点评 本题主要考查半角公式,余弦函数的单调性,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<1}\\{f(x-1),x≥1}\end{array}\right.$,则f(log27)的值为( )
| A. | $\frac{7}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{7}{16}$ |
13.已知i为虚数单位,复数z满足z(2-i)=10+5i,则z等于( )
| A. | 3+4i | B. | 3-4i | C. | -3+4i | D. | -3-4i |
3.执行如图程序框图,若输出的S值为62,则判断框内为( )
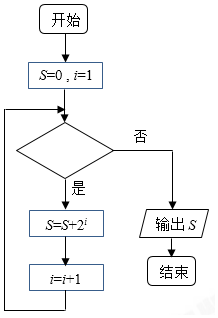

| A. | i≤4? | B. | i≤5? | C. | i≤6? | D. | i≤7? |
7.有一个7人学习合作小组,从中选取4人发言,要求其中组长和副组长至少有一人参加,若组长和副组长同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )
| A. | 720种 | B. | 600种 | C. | 360种 | D. | 300种 |
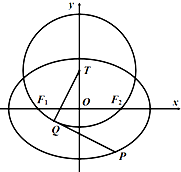 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.