题目内容
6．已知sinα=$\frac{5}{13}$，α∈（$\frac{π}{2}$，π），求sin2α，cos2α的值．分析 由已知及同角三角函数关系式及二倍角的余弦函数公式即可求值．
解答 解：∵sinα=$\frac{5}{13}$，α∈（$\frac{π}{2}$，π），
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{12}{13}$，
∴sin2α=2sinαcosα=2×$\frac{5}{13}×（-\frac{12}{13}）$=-$\frac{120}{169}$，cos2α=2cos2α-1=$\frac{119}{169}$．
点评 本题主要考查了同角三角函数关系式及二倍角的余弦函数公式的应用，属于基本知识的考查．
练习册系列答案
相关题目
17．设a∈R，则“a=1”是“直线ax+y-1=0与直线x+ay+5=0平行”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
1．已知命题p：?x0∈R，x02+2x0+1≤0，则￢p为（ ）
| A． | ?x0∈R，x02+2x0+1＞0 | B． | ?x∈R，x2+2x+1≤0 | ||
| C． | ?x∈R，x2+2x+1≥0 | D． | ?x∈R，x2+2x+1＞0 |
18．函数y=cos2（x+$\frac{π}{2}$）的单调递增区间（ ）
| A． | （kπ，kπ+$\frac{π}{2}$）k∈Z | B． | （kπ+$\frac{π}{2}$，kπ+π）k∈Z | C． | （2kπ，2kπ+π）k∈Z | D． | （2kπ，2kπ+2π）k∈Z |
15．已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，a为双曲线虚轴的一个顶点，过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B，若$\overrightarrow{AB}$=（$\sqrt{2}$-1）$\overrightarrow{AF}$，则此双曲线的离心率是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | $\sqrt{5}$ |
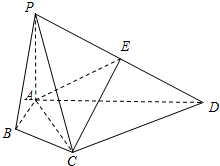在四棱锥P-ABCD中，PA⊥平面ABCD，E是PD的中点，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，AC=AP．