题目内容
7.有一个7人学习合作小组,从中选取4人发言,要求其中组长和副组长至少有一人参加,若组长和副组长同时参加,则他们发言时顺序不能相邻,那么不同的发言顺序有( )| A. | 720种 | B. | 600种 | C. | 360种 | D. | 300种 |
分析 根据题意,分2种情况讨论,①只有甲乙其中一人参加,②甲乙两人都参加,分别求出每一种情况下的情况数目,再由加法原理计算可得答案.
解答 解:根据题意,分2种情况讨论,
①、若甲乙其中一人参加,需要从剩余5人中选取3人,
从甲乙中任取1人,有2种情况,
在剩余5人中任取3人,有C53=10种情况,
将选取的4人,进行全排列,有A44=24种情况,
则此时有2×10×24=480种情况;
②、若甲乙两人都参加,
需要从剩余5人中选取2人,有C52=10种选法,
将甲乙和选出的2人,进行全排列,有A44=24种情况,
则甲乙都参加有10×24=240种情况,
其中甲乙相邻的有C52A44A22A33=120种情况;
则甲乙两人都参加且不相邻的情况有240-120=120种;
则不同的发言顺序种数480+120=600种,
故选:B.
点评 本题考查排列、组合知识,此类问题需要注意常见问题的处理方法,如相邻问题用捆绑法等,本题的关键是根据题意正确进行分类讨论.

练习册系列答案
相关题目
17.设a∈R,则“a=1”是“直线ax+y-1=0与直线x+ay+5=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.函数y=cos2(x+$\frac{π}{2}$)的单调递增区间( )
| A. | (kπ,kπ+$\frac{π}{2}$)k∈Z | B. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z | C. | (2kπ,2kπ+π)k∈Z | D. | (2kπ,2kπ+2π)k∈Z |
15.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,a为双曲线虚轴的一个顶点,过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B,若$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
2.设集合A={x∈N|y=ln(2-x)},B={x|x(x-1)≤0},则A∩B=( )
| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {1} | D. | {0,1} |
19.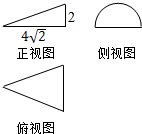 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{8\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}π$ | D. | 8$\sqrt{2}π$ |
17.关于x的不等式(ax+b)(x-2)>0(b>0)的解集为A,记满足(1,2)⊆A的有序实数对(a,b)构成集合N,若向集合M={(a,b)|-1<a<0,0<b<2}所在平面区域内投掷一质点,质点等可能地落在M内任意一点,则该质点恰好落在集合N所在区域内的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
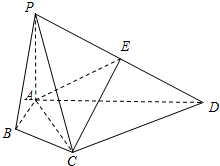 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.