题目内容
9.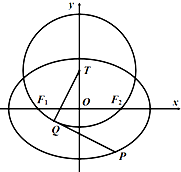 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,若直线3x+4y+5=0上有且仅有一个点M,使得∠F1MF2=90°.(1)求椭圆C的标准方程;
(2)设圆T的圆心T(0,t)在x轴上方,且圆T经过椭圆C两焦点.点P,Q分别为椭圆C和圆T上的一动点.若$\overrightarrow{PQ}•\overrightarrow{QT}$=0时,PQ取得最大值为$\frac{{\sqrt{5}}}{2}$,求实数t的值.
分析 (1)利用椭圆的左,右顶点求出a2,通过圆O与直线3x+4y+5=0相切,求出c,得到b2,然后求解椭圆C的标准方程.
(2)设P(x0,y0),得到$\frac{x_0^2}{2}+y_0^2=1$,设出圆T的方程,利用$\overrightarrow{PQ}•\overrightarrow{QT}=0$,推出PQ2=PT2-QT2=${x_0}^2+{({{y_0}-t})^2}-({{t^2}+1})$,通过①t≥1,②0<t<1,分别求解最大值,得到t的值.
解答 (1)因为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$左,右顶点分别为${A_1}({-\sqrt{2},0}),{A_2}({\sqrt{2},0})$,
所以a2=2. …(1分)
又因为直线3x+4y+5=0上恰存在一个点M,使得∠F1MF2=90°,
即以原点O为圆心,半径为r=OF1=c作圆O,使得圆O与直线3x+4y+5=0相切即可.
又圆心O到直线3x+4y+5=0的距离$d=\frac{{|{3×0+4×0+5}|}}{{\sqrt{{3^2}+{4^2}}}}=1$,…(3分)
所以 c=1,b2=a2-c2=1,…(5分)
所以椭圆C的标准方程为$\frac{x^2}{2}+{y^2}=1$; …(6分)
(2)设P(x0,y0),因为点P在椭圆上,所以有$\frac{x_0^2}{2}+y_0^2=1$,…(7分)
因为圆T的圆心T(0,t)在x轴上方,且圆T经过椭圆C两焦点.
所以圆T的方程为x2+(y-t)2=t2+1,(t>0),…(8分)
由$\overrightarrow{PQ}•\overrightarrow{QT}=0$得PQ2=PT2-QT2=${x_0}^2+{({{y_0}-t})^2}-({{t^2}+1})$,
又$\frac{x_0^2}{2}+y_0^2=1$,所以$P{Q^2}=-{({{y_0}+t})^2}+{t^2}+1$,…(10分)
①当-t≤-1即t≥1时,当y0=-1时,PQ取得最大值$\sqrt{2t}$,
因为PQ的最大值为$\frac{{\sqrt{5}}}{2}$,所以$\sqrt{2t}=\frac{{\sqrt{5}}}{2}$,解得$t=\frac{5}{8}$,又t≥1,故舍去.…(12分)
②当-t>-1即0<t<1时,当y0=-t时,PQ取最大值$\sqrt{{t^2}+1}$,
所以$\sqrt{{t^2}+1}=\frac{{\sqrt{5}}}{2}$,解得${t^2}=\frac{1}{4}$,又0<t<1,所以$t=\frac{1}{2}$.…(14分)
综上,当$t=\frac{1}{2}$时,PQ的最大值为$\frac{{\sqrt{5}}}{2}$.…(16分)
点评 本题考查椭圆的标准方程的求法,椭圆与直线以及圆的方程的综合应用,考查分类讨论转化思想的应用,考查计算能力.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
①设某大学的女生体重y(kg)与身高x(cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的线性回归方程为$\stackrel{∧}{y}$=0.85x-85.71,则若该大学某女生身高增加1cm,则其体重约增加0.85kg;
②命题“?x≥1,x2+3≥4”的否定是“?x<1,x2+3<4”
③相关系数r越小,表明两个变量相关性越弱;
④在一个2×2列联表中,由计算得K2=13.079,则有99%的把握认为这两个变量间有关系;
⑤已知随机变量ξ服从正态分布N(2,σ2),P(ξ≤5)=0.79,则P(ξ≤-1)=0.21;
其中错误的个数是( )
本题可参考独立性检验临界值表:
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | ?x0∈R,x02+2x0+1>0 | B. | ?x∈R,x2+2x+1≤0 | ||
| C. | ?x∈R,x2+2x+1≥0 | D. | ?x∈R,x2+2x+1>0 |
| A. | (kπ,kπ+$\frac{π}{2}$)k∈Z | B. | (kπ+$\frac{π}{2}$,kπ+π)k∈Z | C. | (2kπ,2kπ+π)k∈Z | D. | (2kπ,2kπ+2π)k∈Z |
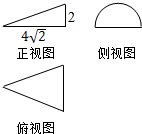 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{8\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}π$ | D. | 8$\sqrt{2}π$ |