题目内容
6.实数x,y满足$\left\{\begin{array}{l}{x+2y-4≤0}\\{x≥1}\\{y≥1}\end{array}\right.$,则z=2x-y的最小值为$\frac{1}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,求目标函数z=2x-y的最小值.
解答 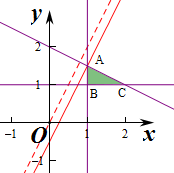 解:由z=2x-y,得y=2x-z,作出不等式对应的可行域(阴影部分),
解:由z=2x-y,得y=2x-z,作出不等式对应的可行域(阴影部分),
平移直线y=2x-z,由平移可知当直线y=2x-z,
经过点A时,直线y=2x-z的截距最大,此时z取得最小值,
由$\left\{\begin{array}{l}{x=1}\\{x+2y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=\frac{3}{2}}\end{array}\right.$,
即A(1,$\frac{3}{2}$),代入z=2-$\frac{3}{2}$=$\frac{1}{2}$,
即目标函数z=2x-y的最小值为$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
17.如图程序框图,若输入a=-9,则输出的结果是( )


| A. | -9 | B. | -3 | C. | 3 | D. | 是负数 |
17.若$\overrightarrow a=\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3}$,$\overrightarrow b=\overrightarrow{e_1}-\overrightarrow{e_2}-\overrightarrow{e_3}$,$\overrightarrow c=\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow d=\overrightarrow{e_1}+2\overrightarrow{e_2}+3\overrightarrow{e_3}$($\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3}$为空间的一个基底)且$\overrightarrow{d}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$+z$\overrightarrow{c}$,则x,y,z分别为( )
| A. | $\frac{5}{2}$,-$\frac{1}{2}$,-1 | B. | $\frac{5}{2}$,$\frac{1}{2}$,1 | C. | -$\frac{5}{2}$,$\frac{1}{2}$,1 | D. | $\frac{5}{2}$,-$\frac{1}{2}$,1 |