��Ŀ����
7��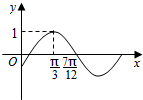 һ��֪����f��x��=cos����x+��-$\frac{��}{2}$�����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x+$\frac{��}{6}$��ȡ����Сֵʱx�ļ���Ϊ��������
һ��֪����f��x��=cos����x+��-$\frac{��}{2}$�����أ�0��|��|��$\frac{��}{2}$���IJ���ͼ����ͼ��ʾ����y=f��x+$\frac{��}{6}$��ȡ����Сֵʱx�ļ���Ϊ��������| A�� | {x|x=k��-$\frac{��}{6}$��k��z} | B�� | {x|x=k��-$\frac{��}{3}$��k��z} | C�� | {x|x=2k��-$\frac{��}{6}$��k��z}} | D�� | {x|x=2k��-$\frac{��}{3}$��k��z}} |
���� ����ͼ����������Ľ���ʽ��������Ǻ��������ʼ��ɵõ����ۣ�
��� �⣺f��x��=cos����x+��-$\frac{��}{2}$��=sin����x+�գ���
��$\frac{T}{4}=\frac{7��}{12}-\frac{��}{3}=\frac{��}{4}$��������f��x��������T=��
��T=$\frac{2��}{��}$=��
���=2����f��x��=sin��2x+�գ���
������Ӧ����2��$\frac{��}{3}$+��=$\frac{��}{2}$��
��æ�=-$\frac{��}{6}$��
��f��x��=sin��2x-$\frac{��}{6}$����
��y=f��x+$\frac{��}{6}$��=sin[2��x+$\frac{��}{6}$��-$\frac{��}{6}$]=sin��2x+$\frac{��}{6}$����
��2x+$\frac{��}{6}$=-$\frac{��}{2}$+2k��
���x=k��-$\frac{��}{3}$��k��z��
��y=f��x+$\frac{��}{6}$��ȡ����Сֵʱx�ļ���Ϊ{x|x=k��-$\frac{��}{3}$��k��z}��
��ѡ��B��
���� ������Ҫ�������Ǻ�����ֵ����⣬����ͼ��������Ǻ����Ľ���ʽ�ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
18����֪����f��x��=tan��2x-$\frac{��}{3}$����������˵��������ǣ�������
| A�� | ����f��x��������Ϊ$\frac{��}{2}$ | |
| B�� | ����f��x����ֵ��ΪR | |
| C�� | �㣨$\frac{��}{6}$��0���Ǻ���f��x����ͼ��һ���Գ����� | |
| D�� | f��$\frac{2��}{5}$����f��$\frac{3��}{5}$�� |
12����ʵ��x��y����$\left\{\begin{array}{l}2x+y��4\\ x��1\\ y��1.\end{array}\right.$��x+3y�����ֵΪ��������
| A�� | 12 | B�� | 7 | C�� | $\frac{9}{2}$ | D�� | 4 |
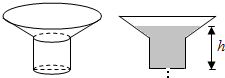 ��ͼ��һ����ת��ɳ©���ϲ�Ϊһ����Բ̨���²�ΪһԲ�����ٶ���
��ͼ��һ����ת��ɳ©���ϲ�Ϊһ����Բ̨���²�ΪһԲ�����ٶ���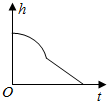
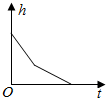
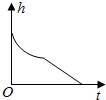
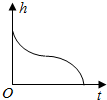
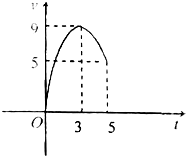 ijУ����������˾��ٱ�����Ҫ������Ļ������ڹ涨�Ĺ����ǰ��5���ӣ����˶�·�̵ij��������������ɼ�����֪ij����������˵��˶��ٶ�v����λ����/�룩��ʱ��t����λ���룩����Ĺ�ϵ������ͼ��ʾ����ô����������˶�5���Ӻ���ʻ��·��s����λ���ף������ǣ�������
ijУ����������˾��ٱ�����Ҫ������Ļ������ڹ涨�Ĺ����ǰ��5���ӣ����˶�·�̵ij��������������ɼ�����֪ij����������˵��˶��ٶ�v����λ����/�룩��ʱ��t����λ���룩����Ĺ�ϵ������ͼ��ʾ����ô����������˶�5���Ӻ���ʻ��·��s����λ���ף������ǣ�������