题目内容
5．已知以点P为圆心的圆经过点A（-1，1）和B（1，3），线段AB的垂直平分线交圆P于点C和D，且|CD|=4．（Ⅰ）求直线CD的方程；
（Ⅱ）求圆P的方程．
分析 （Ⅰ）先求得直线AB的斜率和AB的中点，进而求得CD斜率，利用点斜式取得直线CD 方程．
（Ⅱ）设出圆心P的坐标，利用直线方程列方程，利用点到直线的距离确定a和b的等式综合求得a和b，则圆的方程可得．
解答 解：（Ⅰ）直线AB的斜率k=1，AB中点坐标为（0，2），
∴直线CD的斜率为-1，
∴直线CD方程为y-2=-x，即x+y-2=0
（Ⅱ）设圆心P（a，b），则由P在CD上，得a+b-2=0①
又直径|CD|=4，∴|PA|=2，（a+1）2+（b-1）2②
由①②解得$\left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$或$\left\{\begin{array}{l}a=-1\\ b=3\end{array}\right.$
∴圆心P（1，1）或P（-1，3），
∴圆P的方程为（x-1）2+（y-1）2=4
和（x+1）2+（y-3）2=4．
点评 本题主要考查了直线与圆的方程的应用．考查了学生基础知识的综合运用能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．
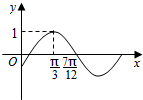一已知函数f（x）=cos（ωx+φ-$\frac{π}{2}$）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则y=f（x+$\frac{π}{6}$）取得最小值时x的集合为（ ）
一已知函数f（x）=cos（ωx+φ-$\frac{π}{2}$）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则y=f（x+$\frac{π}{6}$）取得最小值时x的集合为（ ）| A． | {x|x=kπ-$\frac{π}{6}$，k∈z} | B． | {x|x=kπ-$\frac{π}{3}$，k∈z} | C． | {x|x=2kπ-$\frac{π}{6}$，k∈z}} | D． | {x|x=2kπ-$\frac{π}{3}$，k∈z}} |
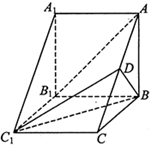在三棱柱ABC-A1B1C1中，侧棱BB1⊥底面A1B1C1，D为AC 的中点，A1B1=BB1=2，A1C1=BC1，∠A1C1B=60°．