设△ABC的内角A.B.C所对的边长分别为a.b.c.已知a=1.b=$\sqrt{3}.A=\frac{π}{6}$.则边长c=2或1．．题目和参考答案——青夏教育精英家教网—

题目内容

19．设△ABC的内角A，B，C所对的边长分别为a，b，c，已知a=1，b=

$\sqrt{3}，A=\frac{π}{6}$ ，则边长c=2或1．．

分析由正弦定理可求sinB= $\frac{\sqrt{3}}{2}$ ，结合范围0＜B＜π，可得B，从而可求C，由正弦定理即可得解．

解答解：∵由正弦定理可得：sinB= $\frac{bsinA}{a}$ = $\frac{\sqrt{3}×sin\frac{π}{6}}{1}$ = $\frac{\sqrt{3}}{2}$ ，
又∵0＜B＜π，
∴B= $\frac{π}{3}$ 或 $\frac{2π}{3}$ ，解得：C=π-A-B= $\frac{π}{2}$ 或 $\frac{π}{6}$ ．
∴c= $\frac{asinC}{sinA}$ = $\frac{1×sinC}{\frac{1}{2}}$ =2sinC=2或1．
故答案为：2或1．

点评本题主要考查了正弦定理的应用，考查了三角形的边角关系的转化，属于基本知识的考查．

练习册系列答案

全国名师点拨小学毕业系统总复习系列答案

中考试题分类精华卷系列答案

第1卷单元月考期中期末系列答案

名校密卷小升初模拟试卷系列答案

68所名校图书小学毕业升学必做的16套试卷系列答案

10．已知全集U=R，集合A={x∈R|-2≤2x≤1}，集合B={x∈R||x|＜1}，则C_U（A∩B）=（　　）

$\frac{1}{2}$ ，+∞）

$\frac{1}{2}$ ]

$\frac{1}{2}$ ，+∞）

$\frac{1}{2}$ ）

7．

一已知函数f（x）=cos（ωx+φ-

$\frac{π}{2}$ ）（ω＞0，|φ|＜

$\frac{π}{2}$ ）的部分图象如图所示，则y=f（x+

$\frac{π}{6}$ ）取得最小值时x的集合为（　　）

$\frac{π}{6}$ ，k∈z}

$\frac{π}{3}$ ，k∈z}

$\frac{π}{6}$ ，k∈z}}

$\frac{π}{3}$ ，k∈z}}

14．已知圆O的半径为r，A为平面上一点，|OA|=a，a≠r，P是圆上任意一点，线段AP的垂直平分线与直线OP相交于点Q，以OA的中点为原点，OA所在直线为x轴建立平面直角坐标系，若Q点轨迹的离心率为

$\sqrt{5}$ ，则（　　）

$\sqrt{5}$ r

$\sqrt{3}$ r

$\sqrt{2}$ r

4．

如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点．
（Ⅰ）求证：平面BDGH∥平面AEF；
（Ⅱ）求CF与平面BDEF所成角的正弦值．

11．已知函数f（x）=（2^x-

$\frac{1}{{2}^{x}}$ ）x，则下列结论中正确的是（　　）

	A．	若-3≤m＜n，则f（m）＜f（n）		B．	若m＜n≤0，则f（m）＜f（n）
	C．	若f（m）＜f（n），则m²＜n²		D．	若f（m）＜f（n），则m³＜n³

8．在△ABC中，sinA：sinC=3：4，∠B=120°，S_△ABC=12

$\sqrt{3}$ ，求a，b，c三边的边长．

17．

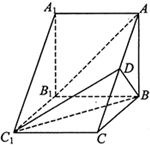在三棱柱ABC-A₁B₁C₁中，侧棱BB₁⊥底面A₁B₁C₁，D为AC 的中点，A₁B₁=BB₁=2，A₁C₁=BC₁，∠A₁C₁B=60°．
（Ⅰ）求证：AB₁∥平面BDC₁；
（Ⅱ）求多面体A₁B₁C₁DBA的体积．