题目内容
18.已知函数f(x)=tan(2x-$\frac{π}{3}$),则下列说法错误的是( )| A. | 函数f(x)的周期为$\frac{π}{2}$ | |
| B. | 函数f(x)的值域为R | |
| C. | 点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心 | |
| D. | f($\frac{2π}{5}$)<f($\frac{3π}{5}$) |
分析 由周期公式可求函数f(x)的周期T=$\frac{π}{2}$;由正切函数的图象和性质可知函数f(x)的值域为R;由2x-$\frac{π}{3}$=kπ,k∈Z可解得:x=$\frac{kπ}{2}+\frac{π}{6}$,k∈Z,可解得点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心;由f($\frac{2π}{5}$)=tan(2×$\frac{2π}{5}$-$\frac{π}{3}$)=tan$\frac{7π}{15}$>0;f($\frac{3π}{5}$)=tan(2×$\frac{3π}{5}$-$\frac{π}{3}$)=tan$\frac{13π}{15}$<0,从而可得f($\frac{2π}{5}$)>f($\frac{3π}{5}$),从而得解.
解答 解:∵f(x)=tan(2x-$\frac{π}{3}$),
∴函数f(x)的周期T=$\frac{π}{2}$,故A正确;
由正切函数的图象和性质可知函数f(x)的值域为R,故B正确;
由2x-$\frac{π}{3}$=kπ,k∈Z可解得:x=$\frac{kπ}{2}+\frac{π}{6}$,k∈Z,则解得:当k=0时,点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心,故C正确;
由f($\frac{2π}{5}$)=tan(2×$\frac{2π}{5}$-$\frac{π}{3}$)=tan$\frac{7π}{15}$>0;f($\frac{3π}{5}$)=tan(2×$\frac{3π}{5}$-$\frac{π}{3}$)=tan$\frac{13π}{15}$<0,从而f($\frac{2π}{5}$)>f($\frac{3π}{5}$),故D不正确.
故选:D.
点评 本题主要考查了正切函数的图象和性质,属于基本知识的考查.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | (-∞,-1]∪($\frac{1}{2}$,+∞) | B. | (-1,$\frac{1}{2}$] | C. | (-∞,-1)∪[-$\frac{1}{2}$,+∞) | D. | (-1,-$\frac{1}{2}$) |
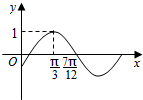 一已知函数f(x)=cos(ωx+φ-$\frac{π}{2}$)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x+$\frac{π}{6}$)取得最小值时x的集合为( )
一已知函数f(x)=cos(ωx+φ-$\frac{π}{2}$)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则y=f(x+$\frac{π}{6}$)取得最小值时x的集合为( )| A. | {x|x=kπ-$\frac{π}{6}$,k∈z} | B. | {x|x=kπ-$\frac{π}{3}$,k∈z} | C. | {x|x=2kπ-$\frac{π}{6}$,k∈z}} | D. | {x|x=2kπ-$\frac{π}{3}$,k∈z}} |
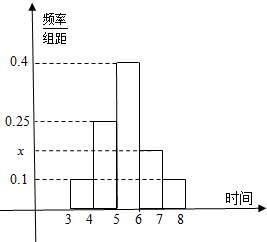 教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.
教育部规定中学生每天体育锻炼不少于一个小时,各个学校认真执行,阳光体育正如火如荼.为了检查学校阳光体育开展情况,从学校随机抽取了20个人,由于项目较多和学生爱好原因,本次检查计算了每人篮球和羽毛球活动时间之和,以这个时间作为该同学的阳光体育活动时间.已知这20个人的阳光体育活动时间都在3小时到8小时之间,并绘制出如图的频率分布直方图.