题目内容
5.已知数列{an}的前n项和为Sn,且a1=2,lg[(n+1)an+1]-lg[(n+2)an]-lg2=0(n∈N*).(Ⅰ) 求数列{an}的通项公式;
(Ⅱ) 设Pn=$\frac{S_n}{{2{a_n}}}$,Tn=$\sqrt{\frac{{1-{P_n}}}{{1+{P_n}}}}$,求证:P1•P3•P5…P2n-1<Tn<$\sqrt{2}sin{T_n}$.
分析 (I)变形$\frac{{{a_{n+1}}}}{n+2}=2•\frac{a_n}{n+1}$,判断$\left\{{\frac{a_n}{n+1}}\right\}$是以首项为$\frac{a_1}{2}=1$,公比为2的等比数列. 求解通项公式.
(II)两式相减,得$-{S_n}=2+2+{2^2}+{2^3}+…+{2^{n-1}}-(n+1)•{2^n}$=$2+\frac{{2({2^{n-1}}-1)}}{2-1}-(n+1)•{2^n}$=-n•2n,
${P_n}=\frac{{n•{2^n}}}{{2•(n+1)•{2^{n-1}}}}=\frac{n}{n+1}$,${T_n}=\sqrt{\frac{{1-\frac{n}{n+1}}}{{1+\frac{n}{n+1}}}}=\sqrt{\frac{1}{2n+1}}$.
方法一:放缩证明${({P_1}•{P_3}•{P_5}…{P_{2n-1}})^2}={(\frac{1}{2})^2}×{(\frac{3}{4})^2}×{(\frac{5}{6})^2}×…×{(\frac{2n-1}{2n})^2}$,${P_1}•{P_3}•{P_5}…{P_{2n-1}}<\sqrt{\frac{1}{2n+1}}$,即可证明.
方法二:用数学归纳法证明如下:按步骤论证即可.
解答 解:(Ⅰ)∵a1=2,lg[(n+1)an+1]-lg[(n+2)an]-lg2=0,
∴$\frac{{(n+1){a_{n+1}}}}{{2(n+2){a_n}}}=1$,即$\frac{{{a_{n+1}}}}{n+2}=2•\frac{a_n}{n+1}$,
∴$\left\{{\frac{a_n}{n+1}}\right\}$是以首项为$\frac{a_1}{2}=1$,公比为2的等比数列.
∴$\frac{a_n}{n+1}={2^{n-1}}$,即${a_n}=(n+1)•{2^{n-1}}$.
(Ⅱ)∵${a_n}=(n+1)•{2^{n-1}}$,∴${S_n}=2+3×2+4×{2^2}+…+(n+1)•{2^{n-1}}$,$2{S_n}=2×2+3×{2^2}+4×{2^3}+…+n{2^{n-1}}+(n+1)•{2^n}$.
两式相减,得$-{S_n}=2+2+{2^2}+{2^3}+…+{2^{n-1}}-(n+1)•{2^n}$=$2+\frac{{2({2^{n-1}}-1)}}{2-1}-(n+1)•{2^n}$=-n•2n,
∴${S_n}=n•{2^n}$.
∵${P_n}=\frac{S_n}{{2{a_n}}}$,${T_n}=\sqrt{\frac{{1-{P_n}}}{{1+{P_n}}}}$,
∴${P_n}=\frac{{n•{2^n}}}{{2•(n+1)•{2^{n-1}}}}=\frac{n}{n+1}$,
${T_n}=\sqrt{\frac{{1-\frac{n}{n+1}}}{{1+\frac{n}{n+1}}}}=\sqrt{\frac{1}{2n+1}}$.
①先证明:P1•P3•P5…P2n-1<Tn.
方法一:∵${P_1}•{P_3}•{P_5}…{P_{2n-1}}=\frac{1}{2}×\frac{3}{4}×\frac{5}{6}×…×\frac{2n-1}{2n}$,
∴${({P_1}•{P_3}•{P_5}…{P_{2n-1}})^2}={(\frac{1}{2})^2}×{(\frac{3}{4})^2}×{(\frac{5}{6})^2}×…×{(\frac{2n-1}{2n})^2}$=$\frac{1}{4}×\frac{9}{16}×\frac{25}{36}×…×\frac{{{{(2n-1)}^2}}}{{{{(2n)}^2}}}$$<\frac{1}{3}×\frac{3}{5}×\frac{5}{7}×…×\frac{2n-1}{2n+1}=\frac{1}{2n+1}$,
∴${P_1}•{P_3}•{P_5}…{P_{2n-1}}<\sqrt{\frac{1}{2n+1}}$,即P1•P3•P5…P2n-1<Tn.
方法二:用数学归纳法证明如下:
(1)当n=1时,左边=${P_1}=\frac{1}{2}$,右边=${T_1}=\sqrt{\frac{1}{3}}=\frac{1}{{\sqrt{3}}}$,
∵$\frac{1}{2}<\frac{1}{{\sqrt{3}}}$,∴左边<右边,即不等式成立.
(2)假设当n=k时,不等式成立,即${P_1}•{P_3}•{P_5}…{P_{2k-1}}<\sqrt{\frac{1}{2k+1}}$,
那么,当n=k+1时,
左边=${P_1}•{P_3}•{P_5}…{P_{2k-1}}•{P_{2k+1}}={P_1}•{P_3}•{P_5}…{P_{2k-1}}•\frac{2k+1}{2k+2}$$<\sqrt{\frac{1}{2k+1}}•\frac{2k+1}{2k+2}=\sqrt{\frac{1}{2k+1}•\frac{{{{(2k+1)}^2}}}{{{{(2k+2)}^2}}}}=\sqrt{\frac{2k+1}{{{{(2k+2)}^2}}}}$$<\sqrt{\frac{(2k+1)}{{{{(2k+2)}^2}-1}}}=\sqrt{\frac{(2k+1)}{(2k+3)(2k+1)}}=\sqrt{\frac{1}{2k+3}}=\sqrt{\frac{1}{2(k+1)+1}}$=Tk+1=右边,
∴左边<右边.∴当n=k+1时,不等式也成立.
∴P1•P3•P5…P2n-1<Tn对n∈N*都成立.
②再证明:${T_n}<\sqrt{2}sin{T_n}$,即证明$\sqrt{\frac{1}{2n+1}}<\sqrt{2}sin\sqrt{\frac{1}{2n+1}}$.
设函数$f(x)=x-\sqrt{2}sinx$,则导函数${f^/}(x)=1-\sqrt{2}cosx$.
令f′(x)=0,得$cosx=\frac{{\sqrt{2}}}{2}$,
∴在$(0,\frac{π}{4})$上有f′(x)<0,即f(x)在$(0,\frac{π}{4})$上单调递减.
∴f(x)<f(0)=0,即$x<\sqrt{2}sinx$在$(0,\frac{π}{4})$上恒成立.
又∵$0<\sqrt{\frac{1}{2n+1}}≤\sqrt{\frac{1}{3}}<\frac{π}{4}$,
∴$\sqrt{\frac{1}{2n+1}}<\sqrt{2}sin\sqrt{\frac{1}{2n+1}}$,即${T_n}<\sqrt{2}sin{T_n}$.
综上可得:${P_1}•{P_3}•{P_5}…{P_{2n-1}}<{T_n}<\sqrt{2}sin{T_n}$.
点评 本题主要考查了等比关系的确定和数列的求和问题.考查了学生对数列知识的综合掌握,综合解决问题的能力,数学式子的变形能力,思维能力,放缩变形能力,难度较大,属于难题.

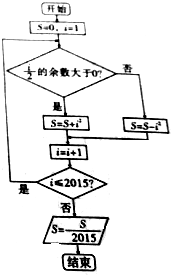
| A. | 1006 | B. | 1008 | C. | 2015 | D. | 2016 |
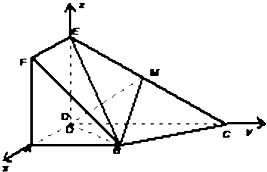 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.