题目内容
14．已知复数z满足|z|=1，则|$\frac{{z}^{2}-2z+2}{z-1+i}$|的最大值为1+$\sqrt{2}$．分析 直接利用平方差公式化简复数的分子，化简复数后利用复数的几何意义求解即可．
解答 解：复数z满足|z|=1，
|$\frac{{z}^{2}-2z+2}{z-1+i}$|=$\left|\frac{（z-1+i）（z-1-i）}{z-1+i}\right|$=|z-1-i|，它的几何意义是单位圆上的点到（1，1）点的距离，
则|$\frac{{z}^{2}-2z+2}{z-1+i}$|的最大值为：$\sqrt{{1}^{2}+{1}^{2}}+1$=1+$\sqrt{2}$．
故答案为：1+$\sqrt{2}$．
点评 本题考查复数模的求法，化简复数以及复数的几何意义是解题的关键．
练习册系列答案
相关题目
12．
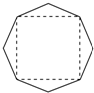某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）
某班设计了一个八边形的班徽（如图），它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形所组成．该八边形的面积为（ ）| A． | 2sin α-2cos α+2 | B． | sin α-$\sqrt{3}$cos α+3 | C． | 3sin α-$\sqrt{3}$cos α+1 | D． | 2sin α-cos α+1 |
如图是三棱柱被平面截去一部分后剩余的几何体的三视图，则截掉的几何体与三视图所示的几何体的体积之比为1：2．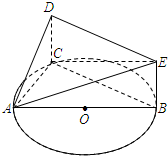
如图，AB是圆O的直径，C是圆O上异于A，B的一个动点，DC垂直于圆O所在的平面，DC∥EB，DC=EB=1，AB=4．
已知A、B分别为曲线C：$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞0）与x轴的左、右两个交点，直线l过点B且与x轴垂直，P为l上异于点B的点，连结AP与曲线C交于点M．