题目内容

10．求|2x+1|+|x-1|的最值．

分析 去掉绝对值符号，化为分段函数，通过数形结合即可求得函数y的最值．

解答 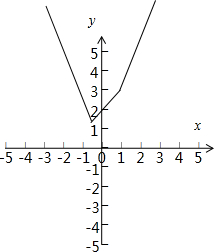解：y=|2x+1|+|x-1|=$\left\{\begin{array}{l}3x，x≥1\\ x+2，-\frac{1}{2}≤x＜2\\-3x，x＜-\frac{1}{2}\end{array}\right.$，
图象如图所示：
有图象可知函数有最小值，最小值为$\frac{3}{2}$．

点评 本题考查绝对值不等式的解法，通过对x的取值分类讨论去掉绝对值符号是关键，考查等价转化思想与数形结合思想的综合运用，考查运算能力，属于中档题．

练习册系列答案
相关题目
8．已知两不同的平面α，β和两条不重合的直线m，n有下列四个命题：
①若m∥n，n⊥α则m⊥α．
②若m⊥α，m⊥β 则α∥β．
③若m⊥α，m∥n，n?β，则α⊥β．
④若m∥α，α∩β=n则m∥n．
其中真命题的有①②③．
1．在△PAB中，已知点$A（{-\sqrt{6}，0}）$、B（$\sqrt{6}$，0），动点P满足|PA|=|PB|+4．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）设M（-2，0），N（2，0），过点N作直线l垂直于AB，且l与直线MP交于点Q，设点Q关于x轴的对称点为R，求证：$\overrightarrow{OP}•\overrightarrow{OR}$为定值；
（Ⅲ）在（II）的条件下，试问x轴上是否存在定点T，使得PN⊥QT．若存在，求出点T的坐标；若不存在，请说明理由．
18．计算：cos$\frac{π}{2015}$cos$\frac{2π}{2015}$cos$\frac{3π}{2015}$…cos$\frac{1007π}{2015}$=$\frac{1}{{2}^{1007}}$．
5．已知数列{an}的前n项和为Sn，且a1=2，lg[（n+1）an+1]-lg[（n+2）an]-lg2=0（n∈N*）．
（Ⅰ） 求数列{an}的通项公式；
（Ⅱ） 设Pn=$\frac{S_n}{{2{a_n}}}$，Tn=$\sqrt{\frac{{1-{P_n}}}{{1+{P_n}}}}$，求证：P1•P3•P5…P2n-1＜Tn＜$\sqrt{2}sin{T_n}$．
15．等比数列的首项是-5，公比是-2，则它的第6项是（　　）
A．-160B．160C．90D．10
2．已知数列{an}、{bn}中，对任何正整数n都有：a1bn+a2bn-1+a3bn-2…+an-1b2+anb1=2n+1-n-2．
（1）若数列{an}是首项和公差都是1的等差数列，求b1，b2，并证明数列{bn}是等比数列；
（2）若数列{bn}是等比数列，数列{an}是否是等差数列，若是请求出通项公式，若不是请说明理由；
（3）若数列{an}是等差数列，数列{bn}是等比数列，求证：$\frac{1}{{a}_{1}{b}_{1}}$+$\frac{1}{{a}_{2}{b}_{2}}$+…+$\frac{1}{{a}_{n}{b}_{n}}$＜$\frac{3}{2}$．
19．如图是三棱柱被平面截去一部分后剩余的几何体的三视图，则截掉的几何体与三视图所示的几何体的体积之比为1：2．
20．已知数列{an}的首项a1=1，an+1=$\frac{3{a}_{n}}{{a}_{n}+1}$，n∈N+．
（Ⅰ）证明：数列{$\frac{1}{{a}_{n}}-\frac{1}{2}$}是等比数列；
（Ⅱ）求数列{$\frac{2n}{{a}_{n}}$}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网