题目内容
15.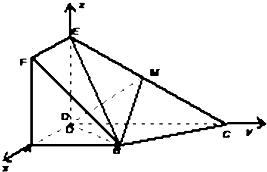 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,当点M为EC中点时.(1)求证:BM∥平面ADEF;
(2)求平面BDM与平面ABF所成锐二面角.
分析 (1)以直线DA、DC、DE分别为x轴、y轴、z轴建立空间直角坐标系,$\overrightarrow{OC}=(0,4,0)$是平面ADEF的一个法向量,证明$\overrightarrow{BM}•\overrightarrow{OC}=0$,即可证明BM∥平面ADEF;
(2)求出平面BDM的一个法向量、平面ABF的一个法向量,利用向量的夹角公式求平面BDM与平面ABF所成锐二面角.
解答 (1)证明:以直线DA、DC、DE分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),B(2,2,0)C(0,4,0),E(0,0,2),M(0,2,1).
∴$\overrightarrow{BM}=(-2,0,1)$--------(2分)
又$\overrightarrow{OC}=(0,4,0)$是平面ADEF的一个法向量.
∵$\overrightarrow{BM}•\overrightarrow{OC}=0$即$\overrightarrow{BM}⊥\overrightarrow{OC}$
∴BM∥平面ADEF------(4分)
(2)解:设M(x,y,z),则$\overrightarrow{EM}=(x,y,z-2)$,
又$\overrightarrow{EC}=(0,4,-2)$
设$\overrightarrow{EM}=\frac{1}{2}\overrightarrow{EC}$,即M(0,2,1).--(6分)
设$\overrightarrow n=({x_1},{y_1},{z_1})$是平面BDM的一个法向量,则$\overrightarrow{OB}•\overrightarrow n=2{x_1}+2{y_1}=0$,$\overrightarrow{OM}•\overrightarrow n=4λ{y_1}+(2-2λ){z_1}=0$
取x1=1得 y1=-1,z1=2即$\overrightarrow n=(1,-1,2)$
又由题设,$\overrightarrow{OA}=(2,0,0)$是平面ABF的一个法向量,
∴$|{cos<\overrightarrow{OA},\overrightarrow n>}|=\frac{{\overrightarrow{OA}•\overrightarrow n}}{{|{\overrightarrow{OA}}|•|{\overrightarrow n}|}}=\frac{2}{{2\sqrt{2+4}}}=\frac{6}{{\sqrt{6}}}$
点评 本题考查线面平行,考查平面BDM与平面ABF所成锐二面角,考查向量方法的运用,考查学生分析解决问题的能力,属于中档题.

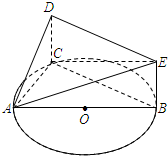 如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A,B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4. 已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.
已知A、B分别为曲线C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>0)与x轴的左、右两个交点,直线l过点B且与x轴垂直,P为l上异于点B的点,连结AP与曲线C交于点M.