题目内容
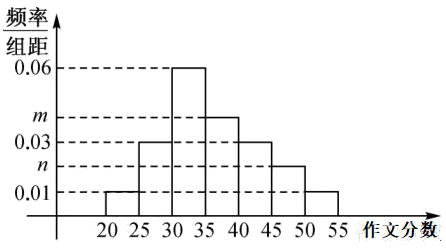
【题目】已知定义在R上的函数f(x)满足f(x+2)=f(x),且当x∈[-1,1]时,f(x)=x2.令g(x)=f(x)-kx-k,若在区间[-1,3]内,函数g(x)=0有4个不相等实根,则实数k的取值范围是( )
A.(0,+∞)B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
令g(x)=0,得f(x)=k(x+1),作出y=f(x)在[1,3]的图象,把函数g(x)=0有4个不相等实根,转化为两个函数的图象的4个交点,利用数形结合法,即可求解,得到答案.
由题意,函数g(x)=f(x)-kx-k,令g(x)=0,得f(x)=k(x+1),
又由函数f(x)满足f(x+2)=f(x),则f(x)的周期为T=2,
作出y=f(x)在[-1,3]的图象,如图所示.
当直线y=k1(x+1)经过点(3,1),则k1=![]() .
.
因为直线y=k(x+1)经过定点(-1,0),且由题意知直线y=k(x+1)与y=f(x)的图象有4个交点,所以0<k≤![]() .
.
故选C.

练习册系列答案
相关题目