题目内容
【题目】已知半径为
的球面上有两点
，且
，球心为
，若
是球面上的动点，且二面角
的大小为
，则四面体
的外接球表面积为______.
【答案】
【解析】
设
所在截面圆的圆心为
，
中点为
，连接
，易知
，
，从而可知
即为二面角
的平面角，
，进而可求出
，
，
，由到
三点的距离相等，可知四面体
外接球的球心
在射线上，设四面体外接球半径为
，在
中，由勾股定理，可得
，可求出，进而求出外接球的表面积.
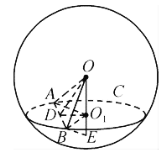
设所在截面圆的圆心为，中点为，连接，
则
，所以，同理，所以即为二面角的平面角，.
因为
，
，所以
是等腰直角三角形，所以
.
在
中，由
，得
，由勾股定理，得
.
因为到三点的距离相等，所以四面体外接球的球心在射线上.
设四面体外接球半径为，在中，
，
，
，由勾股定理，可得，即
，解得
，所以
.
故答案为：.
名校课堂系列答案【题目】江苏省从2021年开始，高考取消文理分科，实行“3＋1＋2”的模式，其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目，某校为了解高一年级学生对“1”的选课情况，随机抽取了100名学生进行问卷调查，如下表是根据调查结果得到的2×2列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | 50 | b | m |
女生 | c | 20 | 40 |
总计 | 100 |
（1）求m，b，c的值；
（2）请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关？说明你的理由.
附：对于2×2列联表
类1 | 类2 | 合计 | |
类A | a | b | a＋b |
类B | c | d | c＋d |
合计 | a＋c | b＋d | a＋b＋c＋d |
有
，其中
.
P( | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】边长为2正方体
中，点E在棱CD上.
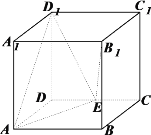
（1）求证：
；
（2）若E是CD中点，求
与平面
所成的角的正弦值；
（3）设M在棱
上，且
，是否存在点E，使平面⊥平面
，若存在，指出点E的位置，若不存在，请说明理由.
【题目】“爱国，是人世间最深层、最持久的情感，是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中，爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造，根据市场调研与模拟，得到科技改造投入
（亿元）与科技改造直接收益
（亿元）的数据统计如下：
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当
时，建立了
与的两个回归模型：模型①：
；模型②：
；当
时，确定与满足的线性回归方程为：
.
（1）根据下列表格中的数据，比较当时模型①、②的相关指数
，并选择拟合精度更高、更可靠的模型，预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
（附：刻画回归效果的相关指数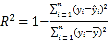
，
.）
（2）为鼓励科技创新，当科技改造的投入不少于20亿元时，国家给予公司补贴收益10亿元，以回归方程为预测依据，比较科技改造投入17亿元与20亿元时公司实际收益的大小；
（附：用最小二乘法求线性回归方程
的系数公式
；
）
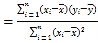（3）科技改造后，“东方红”款汽车发动机的热效率
大幅提高，
服从正态分布
，公司对科技改造团队的奖励方案如下：若发动机的热效率不超过
，不予奖励；若发动机的热效率超过但不超过
，每台发动机奖励2万元；若发动机的热效率超过，每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
（附：随机变量
服从正态分布
，则
，
.）
