题目内容
【题目】已知点![]() ,点P为平面上的动点,过点P作直线l:
,点P为平面上的动点,过点P作直线l:![]() 的垂线,垂足为Q,且
的垂线,垂足为Q,且![]() .
.
![]() Ⅰ
Ⅰ![]() 求动点P的轨迹C的方程;
求动点P的轨迹C的方程;
![]() Ⅱ
Ⅱ![]() 设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足
设点P的轨迹C与x轴交于点M,点A,B是轨迹C上异于点M的不同的两点,且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】![]() Ⅰ
Ⅰ![]() ;
;![]() Ⅱ
Ⅱ![]()
【解析】
![]() Ⅰ
Ⅰ![]() 设
设![]() ,则
,则![]() ,根据
,根据![]() 代入整理即可得P点的轨迹方程;
代入整理即可得P点的轨迹方程;
![]() Ⅱ
Ⅱ![]() 表示出MA方程并与轨迹C联立,可得A的坐标,设出直线AB的方程并与C联立,利用根于系数关系得到
表示出MA方程并与轨迹C联立,可得A的坐标,设出直线AB的方程并与C联立,利用根于系数关系得到![]() 的坐标,进而得到
的坐标,进而得到![]() ,并用换元思想及二次函数最值可求出
,并用换元思想及二次函数最值可求出![]() 范围
范围
![]() Ⅰ
Ⅰ![]() 因为
因为![]() ,设
,设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
整理得![]() ,
,
所以点P的轨迹C的方程为![]()
![]() Ⅱ
Ⅱ![]() 根据题意知
根据题意知![]() ,设MA:
,设MA:![]() ,
,
联立![]() ,解得
,解得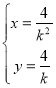 ,所以点
,所以点![]() ,
,
设AB:![]() ,
,
联立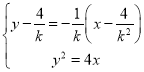 ,消去x得
,消去x得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,
,
则![]() ,
,
所以![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,对称轴为
,对称轴为![]() ,所以y在
,所以y在![]() 上单调递增,
上单调递增,
所以当![]() 时,y取最小值,即
时,y取最小值,即![]() 取最小值,
取最小值,
所以![]() 最小值为
最小值为![]() ,
,
则![]() 最小值为
最小值为![]() ,
,
所以![]() 取值范围是
取值范围是![]()

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目