题目内容
7.已知直线l过点(1,0),且与直线x-y+1=0垂直,若直线l与圆C:x2+y2+2y-3=0相交于A、B两点,则△ABC的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 先求出直线l的方程,再求出圆心C与半径r,计算圆心到直线l的距离d,求出弦长|AB|,再计算△ABC的面积.
解答 解:∵直线l过点(1,0),且与直线x-y+1=0垂直,
设直线l的方程为x+y+m=0,
∴1+0+m=0,
解得m=-1,
∴直线l的方程为x+y-1=0;
又圆C:x2+y2+2y-3=0,
化为标准方程是x2+(y+1)2=4,
∴圆心C(0,-1),半径r=2,
且圆心C到直线l的距离为:
d=$\frac{|0-1-1|}{\sqrt{{1}^{2}{+1}^{2}}}$=$\sqrt{2}$,
∴弦长|AB|=2$\sqrt{{r}^{2}{-d}^{2}}$=2$\sqrt{{2}^{2}{-(\sqrt{2})}^{2}}$=2$\sqrt{2}$,
∴△ABC的面积为S△ABC=$\frac{1}{2}$|AB|d=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2.
故选:C.
点评 本题考查了直线与圆的方程的应用问题,考查了两条直线垂直以及直线与圆相交所得弦长的计算问题,是基础题目.

练习册系列答案
相关题目
17.执行如图所示的程序框图,如果输入的x∈R,则输出的h(x)的最小值是( )


| A. | $\frac{3}{4}$ | B. | 3 | C. | 4 | D. | 7 |
18.已知变量x与y线性相关,数据如表:则y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 6 | 7 |
| A. | (1,3) | B. | (2,6) | C. | (3,7) | D. | (1.5,4) |
15.已知f(x)=|x-2|-1,若直线y=m与函数y=f[f(x)]的图象有四个不同的交点,则实数m的取值范围是( )
| A. | (-1,2) | B. | (0,3) | C. | (-1,1) | D. | (-1,3) |
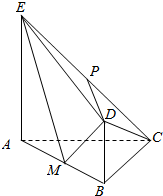 如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.
如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.