题目内容
12.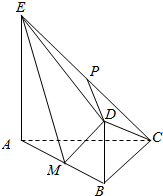 如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.
如图,平面ABDE⊥平面ABC,AC⊥BC,AC=BC=4,四边形ABDE是直角梯形,BD∥AE,BD⊥BA,AE=2BD=4,P、M分别为CE,AB的中点.(Ⅰ)证明:PD∥平面ABC;
(Ⅱ)是否在EM上存在一点N,使得PN⊥平面ABDE.若存在,请指出点N的位置,并加以证明;若不存在,请说明理由.
分析 (I)取AC的中点F,连接PF,BF,根据三角形中位定理及平行四边形的判定及性质,可得PD∥BF,进而由线面平行的判定定理得到PD∥平面ABC;
(II)当N是EM中点时,PN⊥平面ABDE.先证明CM⊥面ABDE,再由PN∥CM,可得PN⊥平面ABDE.
解答 证明:(I)取AC中点F,连接PF、FB.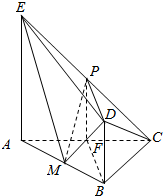
∵F是AC的中点,P为CE的中点,
∴PF∥EA,且PF=$\frac{1}{2}$EA,
又BD∥AE,且BD=$\frac{1}{2}$AE,
∴PF∥DB,PF=DB,
∴四边形BDPF是平行四边形.
∴PD∥FB.
又∵FB?平面ABC,PD?平面ABC,
∴PD∥面ABC.
(II)当N是EM中点时,PN⊥平面ABDE.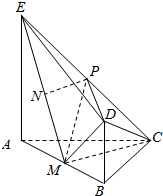
证明:取EM中点N,连接PN、CM,
∵AC=BC,M为AB中点,
∴CM⊥AB,
又∵面ABDE⊥面ABC,面ABDE∩面ABC=AB,CM?面ABC,
∴CM⊥面ABDE,
∵N是EM中点,P为CE中点,
∴PN∥CM,
∴PN⊥平面ABDE.
点评 本题考查证明线面平行、线面垂直的方法,取AC中点F,EM中点 N,是解题的关键.

练习册系列答案
相关题目
7.已知直线l过点(1,0),且与直线x-y+1=0垂直,若直线l与圆C:x2+y2+2y-3=0相交于A、B两点,则△ABC的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
17.已知命题p:?x0∈R,sinx0=$\sqrt{2}$;命题q:?x∈R,x2-x+1>0.则下列结论正确的是( )
| A. | 命题是p∨q假命题 | B. | 命题是p∧q真命题 | ||
| C. | 命题是(?p)∨(?q)真命题 | D. | 命题是(?p)∧(?q)真命题 |
4.已知P为椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点,如果存在过点M(x0,0)(x0>0)的直线交椭圆于A、B两点,使得S△AOB=2S△AOP,则x0的取值范围是( )
| A. | (1,$\sqrt{3}$] | B. | [$\sqrt{3}$,2) | C. | (1,2) | D. | (1,+∞) |

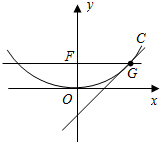 设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).
设p>0,抛物线方程为C:x2=2px.如图所示,过焦点F作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过点(0,-1).