题目内容
19.曲线y=x(2lnx-1)在点(1,-1)处的切线方程为x-y-2=0.分析 因为曲线的切线的斜率是曲线在切点处的导数,所以只需求出曲线在x=1时的导数,再用点斜式写出切线方程,化简即可.
解答 解:对y=x(2lnx-1)求导,得,y′=2lnx+1,
当x=1时,y′=1,
∴曲线y=x(2lnx-1)在点(1,-1)处的切线斜率为-1.
又切点为(1,-1),
∴切线方程为y+1=x-1,
即x-y-2=0,
故答案为:x-y-2=0.
点评 本题主要考查曲线的导数的几何意义,以及直线的点斜式方程.属于基础题.

练习册系列答案
相关题目
9.设函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
7.已知直线l过点(1,0),且与直线x-y+1=0垂直,若直线l与圆C:x2+y2+2y-3=0相交于A、B两点,则△ABC的面积为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
4.已知P为椭圆$\frac{{x}^{2}}{4}$+y2=1的左顶点,如果存在过点M(x0,0)(x0>0)的直线交椭圆于A、B两点,使得S△AOB=2S△AOP,则x0的取值范围是( )
| A. | (1,$\sqrt{3}$] | B. | [$\sqrt{3}$,2) | C. | (1,2) | D. | (1,+∞) |
11.一个算法的程序框图如图所示,若该程序输出的结果为$\frac{5}{6}$,则判断框中应填入的条件是( )


| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
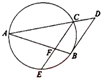 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.