题目内容
16.设a,b∈R,a≠0,在平面直角坐标系xOy中,若两条曲线y=$\frac{a+2}{x}$,y=ax+2b+1在区间[3,4]上至少有一个公共点,则a2+b2的最小值为$\frac{1}{100}$.分析 由题意两条曲线在区间[3,4]上至少有一个公共点,得到$\frac{a+2}{x}$=x+2b+1有解,转化为关于a,b的直线方程(x2-1)a+2bx+x-2=0,得到a2+b2表示原点到直线的距离的平方,转化为a2+b2=d2=($\frac{x-2}{{x}^{2}+1}$)2,巧换元,构造函数,利用函数的单调性质,求出最值.
解答 解:∵曲线y=$\frac{a+2}{x}$,y=ax+2b+1,
∴$\frac{a+2}{x}$=ax+2b+1,
∴a+2=ax2+2bx+x,
∴(x2-1)a+2bx+x-2=0,
于是可以看作关于a,b的直线方程,则(a,b)是该直线上的点,
则a2+b2表示原点到直线的距离的平方,
设原点到直线的距离为d,根据到点直线的距离公式得到
d=$\frac{|x-2|}{\sqrt{({x}^{2}-1)^{2}+4{x}^{2}}}$
∴a2+b2=d2=$\frac{(x-2)^{2}}{({x}^{2}+1)^{2}}$=($\frac{x-2}{{x}^{2}+1}$)2,
令t=x-2,x∈[3,4],则t∈[1,2],则x=t+2,
∴a2+b2=d2=($\frac{t}{(t+2)^{2}+1}$)2=($\frac{t}{{t}^{2}+4t+5}$)2=($\frac{1}{t+\frac{5}{t}+4}$)2,
设f(t)=t+$\frac{5}{t}$+4,t∈[1,2],
∴f′(t)=1-$\frac{5}{{t}^{2}}$<0在∈[1,2]恒成立,
∴函数f(t)在∈[1,2]为减函数,
∴当t=1时,f(t)max=f(1)=1+5+4=10,
∴当t=1时,a2+b2最小值为$\frac{1}{100}$.
故答案为:$\frac{1}{100}$.
点评 本题考查二次函数的性质、函数的单调性及不等式知识,考查学生灵活运用知识解决问题的能力,能力要求较高.

| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
| A. | (1,$\sqrt{3}$] | B. | [$\sqrt{3}$,2) | C. | (1,2) | D. | (1,+∞) |

| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |

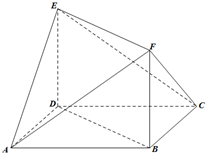 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,