题目内容
如图，PA⊥平面ABC，AE⊥PB，AB⊥BC， AF⊥PC，PA=AB=BC=2.
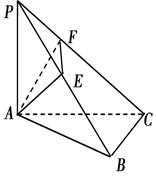
（1）求证：平面AEF⊥平面PBC；
（2）求二面角P-BC-A的大小；
（3）求三棱锥P-AEF的体积.
（1）求证：平面AEF⊥平面PBC；
（2）求二面角P-BC-A的大小；
（3）求三棱锥P-AEF的体积.
（1）略
（2）45°
（3）V=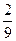
（2）45°
（3）V=
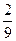
略
练习册系列答案
全优点练单元计划系列答案
相关题目
全优点练单元计划系列答案题目内容
全优点练单元计划系列答案
，
，
，
，
，
，直线
和平面
所成的角为
．
；
的大小．
、
，则
=m，n
中，
分别为各边的中点，
分别为
的中点，将
沿 
折成三棱锥后，
与
所成的角的度数为＿＿＿＿。 
，⊙O为其内切圆，D为BC的中点，将三角形ACD沿AD折叠，使二面角B－AD－C成直二面角，则⊙O上的圆弧扫过的曲面面积为____________．
，
，
，垂足分别为
，
，且
.如果增加一个条件就能推出
，给出四个条件：①
；②
；③
与
在
内的正投影在同一条直线上 ；④