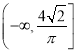Question

【题目】已知双曲线E： ﹣ =1（a＞0，b＞0）的两条渐近线分别为l1：y=2x，l2：y=﹣2x．

（1）求双曲线E的离心率；
（2）如图，O为坐标原点，动直线l分别交直线l1 ， l2于A，B两点（A，B分别在第一、第四象限），且△OAB的面积恒为8，试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程，若不存在，说明理由．

Answer 1

【答案】
（1）解：因为双曲线E的渐近线分别为l1：y=2x，l2：y=﹣2x，

所以 =2．

所以 =2．

故c= a，

从而双曲线E的离心率e= =

（2）解：由（1）知，双曲线E的方程为 ﹣ =1．

设直线l与x轴相交于点C，

当l⊥x轴时，若直线l与双曲线E有且只有一个公共点，则|OC|=a，|AB|=4a，

所以 |OC||AB|=8，

因此 a4a=8，解得a=2，此时双曲线E的方程为 ﹣ =1．

以下证明：当直线l不与x轴垂直时，双曲线E的方程为 ﹣ =1也满足条件．

设直线l的方程为y=kx+m，依题意，得k＞2或k＜﹣2；

则C（﹣ ，0），记A（x1，y1），B（x2，y2），

由 得y1= ，同理得y2= ，

由S△OAB= |OC||y1﹣y2|得：

|﹣ || ﹣ |=8，即m2=4|4﹣k2|=4（k2﹣4）．

由 得：（4﹣k2）x2﹣2kmx﹣m2﹣16=0，

因为4﹣k2＜0，

所以△=4k2m2+4（4﹣k）（m2+16）=﹣16（4k2﹣m2﹣16），

又因为m2=4（k2﹣4），

所以△=0，即直线l与双曲线E有且只有一个公共点．

因此，存在总与直线l有且只有一个公共点的双曲线E，且E的方程为 ﹣ =1

【解析】（1）依题意，可知 =2，易知c= a，从而可求双曲线E的离心率；（2）由（1）知，双曲线E的方程为 ﹣ =1，设直线l与x轴相交于点C，分l⊥x轴与直线l不与x轴垂直讨论，当l⊥x轴时，易求双曲线E的方程为 ﹣ =1．当直线l不与x轴垂直时，设直线l的方程为y=kx+m，与双曲线E的方程联立，利用由S△OAB= |OC||y1﹣y2|=8可证得：双曲线E的方程为 ﹣ =1，从而可得答案．