Question

【题目】如图，在四棱锥中，底面是正方形，侧面⊥底面，若分别为的中点．

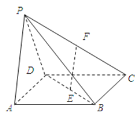
（Ⅰ）求证：平面；

（Ⅱ）求证：平面⊥平面．

Answer 1

【答案】（1）根据题意，证明线面平行，关键是先证明线线平行，即

（2）对于面面垂直的证明，一般先证明线面垂直，，结合面面垂直的判定定理来得到。

【解析】

（Ⅰ）利用线面平行的判定定理，只需证明EF∥PA，即可．

（Ⅱ）先证明线面垂直，CD⊥平面PAD，再证明面面垂直，平面PAD⊥平面PDC即可．

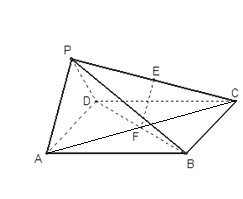
（Ⅰ）证明：连结AC，在正方形ABCD中，F为BD中点，正方形对角线互相平分，

∴F为AC中点，又E是PC中点，在△CPA中，EF∥PA，且PA平面PAD，

EF平面PAD， ∴EF∥平面PAD．

（Ⅱ）∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，CD⊥AD，

平面 ∴CD⊥平面PAD，∵CD平面PDC， ∴平面PAD⊥平面PDC