题目内容
直线y=3x+1与圆x2+y2=4相交于A,B两点,则AB的中点的坐标是______.
设A(x1,y1),B(x2,y2),
联立直线与圆方程得:
,
消去y得:10x2+6x-3=0,
∴x1+x2=-
,即AB中点横坐标为
=-
,
将x=-
代入y=3x+1得:y=
,
则AB中点坐标为(-
,
).
故答案为:(-
,
)
联立直线与圆方程得:
|
消去y得:10x2+6x-3=0,
∴x1+x2=-
| 3 |
| 5 |
| x1+x2 |
| 2 |
| 3 |
| 10 |
将x=-
| 3 |
| 10 |
| 1 |
| 10 |
则AB中点坐标为(-
| 3 |
| 10 |
| 1 |
| 10 |
故答案为:(-
| 3 |
| 10 |
| 1 |
| 10 |

练习册系列答案
相关题目
 ,若分别以
,若分别以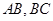 为弦作两外切的圆
为弦作两外切的圆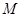 和圆
和圆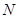 ,且两圆半径相等,则圆的半径为 .
,且两圆半径相等,则圆的半径为 .