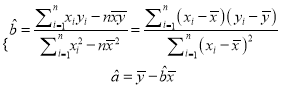题目内容
【题目】已知各项都是正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,求证:
,求证:![]() ;
;
(3)若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)详见解析(Ⅲ)
(Ⅱ)详见解析(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)由和项求数列通项,注意分类讨论:当![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,得数列递推关系式,因式分解可得
,得数列递推关系式,因式分解可得![]() ,根据等差数列定义得数列通项公式
,根据等差数列定义得数列通项公式![]() (Ⅱ)因为
(Ⅱ)因为![]() ,所以利用叠加法求通项公式:
,所以利用叠加法求通项公式:![]() ,因此
,因此![]() ,从而利用裂项相消法求和得
,从而利用裂项相消法求和得![]() ,即证得
,即证得![]() (Ⅲ)不等式恒成立问题,一般先变量分离,转化为求对应函数最值问题:由
(Ⅲ)不等式恒成立问题,一般先变量分离,转化为求对应函数最值问题:由![]() 得
得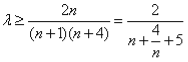 ,而
,而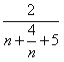 有最大值
有最大值![]() ,所以
,所以![]()
试题解析:(1)![]() 时,
时,![]()

![]()
![]()
![]()
![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列
![]() …4分
…4分
(2)![]()
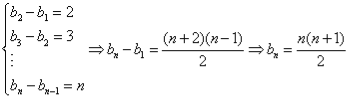
![]() ,
,![]() ,即
,即![]() …………………9分
…………………9分
(3)由![]() 得
得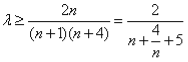 , 当且仅当
, 当且仅当![]() 时,
时,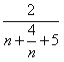 有最大值
有最大值![]() ,
,![]() ………………………………14分
………………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)已知产量![]() 和能耗
和能耗![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: