题目内容
如果一个函数f(x)满足:
(1)定义域为R;
(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0;
(3)任意x∈R,若t>0,f(x+t)>f(x).
则f(x)可以是( )
(1)定义域为R;
(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0;
(3)任意x∈R,若t>0,f(x+t)>f(x).
则f(x)可以是( )
| A.y=-x | B.y=3x | C.y=x3 | D.y=log3x |
由条件(1)定义域为R,排除D;
由条件(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0,即任意x∈R,f(-x)+f(x)=0,即函数f(x)为奇函数,排除B
由条件(3)任意x∈R,若t>0,f(x+t)>f(x).即x+t>x时,总有f(x+t)>f(x),即函数f(x)为R上的单调增函数,排除A
故选 C
由条件(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0,即任意x∈R,f(-x)+f(x)=0,即函数f(x)为奇函数,排除B
由条件(3)任意x∈R,若t>0,f(x+t)>f(x).即x+t>x时,总有f(x+t)>f(x),即函数f(x)为R上的单调增函数,排除A
故选 C

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
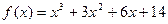 ,且
,且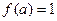 ,
,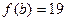 ,则
,则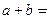 ( )
( )