题目内容
已知函数f（x）=aln（x+1）-x2，若在区间（0，1）内任取两个不同实数m，n，不等式
＜1恒成立，则实数a的取值范围是______．
| f(m+1)-f(n+1) |
| m-n |
由于
=
，则表示点（m+1，f（m+1）） 与点（n+1，f（n+1））连线的斜率，因实数p，q在区间（0，1）内，故m+1和n+1在区间（1，2）内．
∵不等式
=
，恒成立，
∴函数图象上在区间（1，2）内任意两点连线的斜率小于1，
故函数的导数小1在（1，2）内恒成立．
由函数的定义域知，x＞-1，
∴f′（x）=
-2x＜1 在（1，2）内恒成立．
即 a＜2x2+3x+1在（1，2）内恒成立．
由于二次函数y=2x2+3x+1在[1，2]上是单调增函数，
故 x=1时，y=2x2+3x+1 在[1，2]上取最小值为6，
∴a≤6，
故答案为：a≤6．
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
∵不等式
| f(m+1)-f(n+1) |
| m-n |
| f(m+1)-f(n+1) |
| (m+1)-(n+1) |
∴函数图象上在区间（1，2）内任意两点连线的斜率小于1，
故函数的导数小1在（1，2）内恒成立．
由函数的定义域知，x＞-1，
∴f′（x）=
| a |
| x+1 |
即 a＜2x2+3x+1在（1，2）内恒成立．
由于二次函数y=2x2+3x+1在[1，2]上是单调增函数，
故 x=1时，y=2x2+3x+1 在[1，2]上取最小值为6，
∴a≤6，
故答案为：a≤6．
练习册系列答案
相关题目
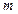为非零实数，若函数
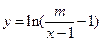的图象关于原点中心对称，则