题目内容
已知函数f(x)=ln
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)对于x∈[2,6],f(x)=ln
>ln
恒成立,求实数m取值范围.
| x+1 |
| x-1 |
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)对于x∈[2,6],f(x)=ln
| x+1 |
| x-1 |
| m |
| (x-1)(7-x) |
(1)由
>0,解得x<-1或x>1,∴定义域为(-∞,-1)∪(1,+∞)(2分)
当x∈(-∞,-1)∪(1,+∞)时,f(-x)=ln
=ln
=ln(
)-1=-ln
=-f(x)
∴f(x)=ln
是奇函数.….(5分)
(2)由x∈[2,6]时,f(x)=ln
>ln
恒成立,
∴
>
>0,
∵x∈[2,6],∴0<m<(x+1)(7-x)在x∈[2,6]成立…(8分)
令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6],
由二次函数的性质可知x∈[2,3]时函数单调递增,x∈[3,6]时函数单调递减,
∴x∈[2,6]时,g(x)min=g(6)=7
∴0<m<7….(12分)
| x+1 |
| x-1 |
当x∈(-∞,-1)∪(1,+∞)时,f(-x)=ln
| -x+1 |
| -x-1 |
| x-1 |
| x+1 |
| x+1 |
| x-1 |
| x+1 |
| x-1 |
∴f(x)=ln
| x+1 |
| x-1 |
(2)由x∈[2,6]时,f(x)=ln
| x+1 |
| x-1 |
| m |
| (x-1)(7-x) |
∴
| x+1 |
| x-1 |
| m |
| (x-1)(7-x) |
∵x∈[2,6],∴0<m<(x+1)(7-x)在x∈[2,6]成立…(8分)
令g(x)=(x+1)(7-x)=-(x-3)2+16,x∈[2,6],
由二次函数的性质可知x∈[2,3]时函数单调递增,x∈[3,6]时函数单调递减,
∴x∈[2,6]时,g(x)min=g(6)=7
∴0<m<7….(12分)

练习册系列答案
相关题目
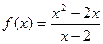 是奇函数
是奇函数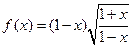 是偶函数
是偶函数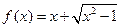 是非奇非偶函数
是非奇非偶函数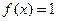 既是奇函数又是偶函数
既是奇函数又是偶函数