题目内容
已知函数f(x)=ax+lnx,a∈R.
(1)讨论y=f(x)的单调性;(2)若定义在区间D上的函数y=g(x)对于区间D上的任意两个值x1、x2总有不等式
[g(x1)+g(x2)]≥g(
)成立,则称函数y=g(x)为区间D上的“凹函数”.
试证明:当a=-1时,g(x)=|f(x)|+
为“凹函数”.
(1)讨论y=f(x)的单调性;(2)若定义在区间D上的函数y=g(x)对于区间D上的任意两个值x1、x2总有不等式
| 1 |
| 2 |
| x1+x2 |
| 2 |
试证明:当a=-1时,g(x)=|f(x)|+
| 1 |
| x |
(1)当a=0时,函数f(x)=lnx在(0,+∞)上是增函数;…(1分)
由已知,x∈(0,+∞),f′(x)=a+
=
,…(3分)
当a>0时,f'(x)>0,函数f(x)在(0,+∞)上是增函数;…(4分)
当a<0时,解f′(x)=
>0得0<x<-
,解f'(x)<0得x>-
,
所以函数f(x)在(0,-
)上是增函数,在(-
,+∞)上是减函数.…(5分)
综上,当a≥0时,函数f(x)在(0,+∞)上是增函数;
当a<0时,函数f(x)在(0,-
)上是增函数,在(-
,+∞)上是减函数.
(2)当a=-1时,由(1)知f(x)在(0,+∞)上的最大值为f(1)=-1,即f(x)<0恒成立.
所以g(x)=|f(x)|+
=-f(x)+
=
+x-lnx,x∈(0,+∞).…(6分)
设x1,x2∈(0,+∞),
计算
[g(x1)+g(x2)]=
(
+x1-lnx1+
+x2-lnx2)=
+
-ln
,g(
)=
+
-ln
,
因为
≥
,所以ln
≥ln
,-ln
≤-ln
,…(8分)
-
=
=
≤0,所以
≤
,…(10分)
所以
[g(x1)+g(x2)]≥g(
),即当a=-1时,g(x)=|f(x)|+
为“凹函数”.
由已知,x∈(0,+∞),f′(x)=a+
| 1 |
| x |
| ax+1 |
| x |
当a>0时,f'(x)>0,函数f(x)在(0,+∞)上是增函数;…(4分)
当a<0时,解f′(x)=
| ax+1 |
| x |
| 1 |
| a |
| 1 |
| a |
所以函数f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
综上,当a≥0时,函数f(x)在(0,+∞)上是增函数;
当a<0时,函数f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
(2)当a=-1时,由(1)知f(x)在(0,+∞)上的最大值为f(1)=-1,即f(x)<0恒成立.
所以g(x)=|f(x)|+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
设x1,x2∈(0,+∞),
计算
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| 2x1x2 |
| x1+x2 |
| 2 |
| x1x2 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
因为
| x1+x2 |
| 2 |
| x1x2 |
| x1+x2 |
| 2 |
| x1x2 |
| x1+x2 |
| 2 |
| x1x2 |
| 2 |
| x1+x2 |
| x1+x2 |
| 2x1x2 |
| 4x1x2-(x1+x2)2 |
| 2x1x2(x1+x2) |
| -(x1-x2)2 |
| 2x1x2(x1+x2) |
| 2 |
| x1+x2 |
| x1+x2 |
| 2x1x2 |
所以
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| x |

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
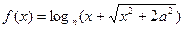 是奇函数,则a= .
是奇函数,则a= .