题目内容
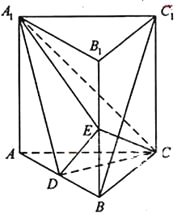
【题目】如图,五面体ABCDE中,四边形ABDE是菱形,△ABC是边长为2的正三角形,∠DBA=60°, ![]() .
. 
(1)证明:DC⊥AB;
(2)若点C在平面ABDE内的射影H,求CH与平面BCD所成的角的正弦值.
【答案】
(1)证明:如图,取AB的中点O,连OC,OD,
因为△ABC是边长为2的正三角形,所以 ![]() ,
,
又四边形ABDE是菱形,∠DBA=60°,所以△DAB是正三角形,
所以 ![]() ,
,
而OD∩OC=O,所以AB⊥平面DOC,
所以AB⊥CD.
(2)解:由(1)知OC=CD,平面DOC⊥平面ABD,
因为平面DOC与平面ABD的交线为OD,
所以点C在平面ABDE内的射影H必在OD上,
所以H是OD的中点,
如图所示建立空间直角坐标系O﹣xyz, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
设平面BDC的法向量为 ![]() ,则
,则  ,取
,取 ![]() ,则x=3,z=1,
,则x=3,z=1,
即平面BCD的一个法向量为 ![]() .
.
所以CH与平面BCD所成的角的正弦值为  =
= ![]() .
.

【解析】(1)取AB的中点O,连OC,OD,证明:AB⊥平面DOC,即可证明DC⊥AB;(2)若点C在平面ABDE内的射影H,建立空间直角坐标系,利用向量方法求CH与平面BCD所成的角的正弦值.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

练习册系列答案
相关题目