Question

【题目】如图，椭圆 的离心率为 ，顶点为A1、A2、B1、B2 ， 且 ．

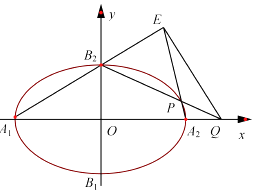
（1）求椭圆C的方程；
（2）P是椭圆C上除顶点外的任意点，直线B2P交x轴于点Q，直线A1B2交A2P于点E．设A2P的斜率为k，EQ的斜率为m，试问2m﹣k是否为定值？并说明理由．

Answer 1

【答案】
（1）

解：由 ，则 ，

由题意及图可得A1（﹣a，0），B1（0，﹣b），B2（0，b），

∴

又 ，则a2﹣b2=3，∴

∴

∴椭圆C的方程为： ；

（2）

解：证明：由题意可知A1（﹣2，0），A2（2，0），B1（0，﹣1），B2（0，1），

由A2P的斜率为k，则直线A2P的方程为y=k（x﹣2），

由 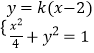，得（1+4k2）x2﹣16k2x+16k2﹣4=0，

其中 ，则 ， ，

则直线B2P的方程为 = （ ），

令y=0，则 ，即

直线A1B2的方程为x﹣2y+2=0，

由 解得 ，则 ，

则EQ的斜率 ，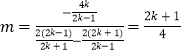

∴ （定值），

2m﹣k为定值 ．

【解析】（1）由椭圆的离心率公式，根据向量数量积的坐标运算，即可求得c的值，求得a的值，即可求得椭圆的标准方程；（2）直线A2P的方程为y=k（x﹣2），代入椭圆方程，求得P点坐标，直线B2P的方程为 = （ ），求得Q点坐标，联立求得E点坐标，求得m，则 （定值）．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．